早教吧作业答案频道 -->数学-->
CO是△ACE的高,点B在OE上,OB=OA,AC=BE(1)如图1,求证:∠A=2∠E;(2)如图2,CF是△ACE的角平分线.①求证:AC+AF=CE;②判断三条线段CE、EF、OF之间的数量关系,并给出证明.
题目详情
CO是△ACE的高,点B在OE上,OB=OA,AC=BE
(1)如图1,求证:∠A=2∠E;
(2)如图2,CF是△ACE的角平分线.
①求证:AC+AF=CE;
②判断三条线段CE、EF、OF之间的数量关系,并给出证明.
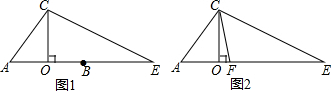
(1)如图1,求证:∠A=2∠E;
(2)如图2,CF是△ACE的角平分线.
①求证:AC+AF=CE;
②判断三条线段CE、EF、OF之间的数量关系,并给出证明.

▼优质解答
答案和解析
证明:(1)连接CB,由AO=OB,CO⊥AB,
∴CA=CB,
∴∠A=∠CBA,
∵AC=BE,
∴BE=CB,
∴∠E=∠BCE,
∴∠A=∠CBA=∠BCE+∠E=2∠E;
(2)①在CE上截取CH=CA,连接FH,
∵∠ACF=∠ECF,CF=CF,
在△FCA与△FCH中,
,
∴△FCA≌△FCH,
∴AF=HF,∠A=∠CHF=∠HFE+∠E=2∠E,
∴∠HFE=∠E,
∴AF=HE,
即CE=CH+HE=CA+AF;
②在①的基础上,BE=AC,AO=OB,
∴CE=CA+AF
=BE+AO+OF
=EF-FB+OB+OF
=EF+OF+OF
=EF+2OF.
∴CA=CB,
∴∠A=∠CBA,
∵AC=BE,
∴BE=CB,
∴∠E=∠BCE,
∴∠A=∠CBA=∠BCE+∠E=2∠E;
(2)①在CE上截取CH=CA,连接FH,
∵∠ACF=∠ECF,CF=CF,
在△FCA与△FCH中,
|
∴△FCA≌△FCH,
∴AF=HF,∠A=∠CHF=∠HFE+∠E=2∠E,
∴∠HFE=∠E,
∴AF=HE,
即CE=CH+HE=CA+AF;
②在①的基础上,BE=AC,AO=OB,
∴CE=CA+AF
=BE+AO+OF
=EF-FB+OB+OF
=EF+OF+OF
=EF+2OF.
看了 CO是△ACE的高,点B在O...的网友还看了以下:
已知ABCD是平行四边形,P点是ABCD所在平面外的一点,连接PA、PB、PC、PD.设点E、F、 2020-05-13 …
已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于 2020-05-15 …
设X是随机变量,C是常数,D(X)存在,试证:对于任意C≠E(X)必有E(X-C)^2>D(X). 2020-06-05 …
设n阶矩阵A=E-a*a^T,其中a是n维非零列向量,证明1.A^2=A的充要条件是a^T*a设n 2020-06-23 …
我想请问根据E=F/qφ=E/q如果要判断E或者φ的大小已知E判断φ用φ=E/qE大φ就大反之.已 2020-07-20 …
连续随机变量X,Y相互独立试用期望值的定义来证明E{exp(t(X+Y))}=E{exp(tX)} 2020-07-23 …
已知向量ā≠ē,|ē|=1,对任意t∈R,恒有|ā-tē|≥|ā-ē|,则ā与ē的关系两边平方并整 2020-08-01 …
高三向量证明三角形中垂线交于一点已知:△ABC,E,F分别为AC与AB的中点,过点E作直线垂直AC 2020-08-01 …
各项同性材料的三个弹性常数E、G、V之间的关系G=E/2(1+V)如何证明?E是弹性模量G是剪切弹性 2020-11-02 …
用初等方法证明E^x-1的等价无穷小量是x.我看一些用罗比特法则证明的,感觉不对,因为求导过程中,计 2020-11-04 …