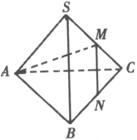
在正三棱锥S-ABC中，M、N分别为棱SC、BC的中点，AM⊥MN若SA=，则此正三棱锥的外接球表面积为.
，则此正三棱锥的外接球表面积为_____________. 
9π
解析：本题考查空间关系的论证及空间想象能力；由题意可知MN∥SB，故AM⊥MN 
AM⊥SB，又在正三棱锥中易证SB⊥AC，即直线加上平面SAC，从而正三棱锥的三条侧棱两两垂直(垂直关系的推导也可由向量推出)，将此正三棱锥可赴形成以S点所在的三条侧棱为边的正方体，那么此正方体即为三棱锥外接球的内接正方体，显然此正方体的体对角线即为外接球的直径，即：(2R) 2 =( ) 2 +( ) 2 +( ) 2 =9，故外接球的表面积为S=4πR 2 =9π．
设△ABC的三边为a，b，c，三边上的高分别为ha，hb，hc，若三边满足2b=a+c，则三个高应 2020-05-13 …
如图，在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c则a，b，c满足的关系 2020-05-13 …
速求此三道几何题答案,1.已知一个三角形的三边为a,b,c,且a小于等于b小于等于c,周长l,求变 2020-05-20 …
已知三角形△ABC三角A、B、C所对应的三边为a、b、c,acosc+√3asinc-b-c=0, 2020-06-03 …
帮我看看几道题↓如下(定有重谢)初2本人绝对诚信,1.在RT三角形中,角A为60度;c+b=21, 2020-06-06 …
已知三角形的三边为a,d,c,它的周长为12cm且c+a=2b,c-a=2cm,求a,b,c的值 2020-06-27 …
关于判断三角形成立的证明设三角形的三边为a,b,c则三角形成立的条件为“任意两边的和大于第三边”且 2020-07-09 …
解三角型已知三角形ABC的三个内角为A,B,C,所对的三边为a,b,c,若面积为S=a^2-(b- 2020-07-19 …
三角函数题设△ABC的三边为a、b、c,对应角是A、B、C,若方程Ax²-（B+C)x+A=0,有 2020-07-30 …
1.已知三角形的三边为a,b,c,它的周长为12cm,且c+a=2b,c-a=2cm,求a,b,c 2020-08-03 …