早教吧作业答案频道 -->数学-->
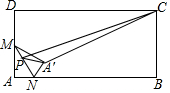
如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是.
题目详情
如图,在矩形ABCD中,AB=4,AD=2,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C.在MN上存在一动点P.连接A'P、CP,则△A'PC周长的最小值是___.

▼优质解答
答案和解析
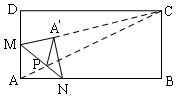 分两步:
分两步:
①连接AP,则AP=AP′,
∴△A'PC周长=A′P+PC+A′C=AP+PC+A′C,
∵AP+PC>AC,
当A、P、C三点共线时,AP+PC有最小值,是AC的长,
所以AC与MN的交点就是点P,
由勾股定理得:AC=
=2
,
②连接CM,
∵A′C>CM-A′M,
∴当M、A′、C三点共线时,A′C有最小值,
此时,∵M是AD的中点,
∴AM=DM=1,
∴MC=
=
,
由折叠得:AM=A′M=1,
∴A′C=MC-A′M=
-1,
∴△A'PC周长的最小值是:
-1+2
,
故答案为:
-1+2
.
 分两步:
分两步:①连接AP,则AP=AP′,
∴△A'PC周长=A′P+PC+A′C=AP+PC+A′C,
∵AP+PC>AC,
当A、P、C三点共线时,AP+PC有最小值,是AC的长,
所以AC与MN的交点就是点P,
由勾股定理得:AC=
| 22+42 |
| 5 |
②连接CM,
∵A′C>CM-A′M,
∴当M、A′、C三点共线时,A′C有最小值,
此时,∵M是AD的中点,
∴AM=DM=1,
∴MC=
| 42+12 |
| 17 |
由折叠得:AM=A′M=1,
∴A′C=MC-A′M=
| 17 |
∴△A'PC周长的最小值是:
| 17 |
| 5 |
故答案为:
| 17 |
| 5 |
看了 如图,在矩形ABCD中,AB...的网友还看了以下:
如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/ 2020-04-26 …
如图,平面直角坐标系中,直线AB:y=−13x+b交y轴于点A(0,1),交x轴于点B.直线x=1 2020-06-08 …
如图,已知点A(-m,n),B(0,m),且m、n满足m+5+(n-5)2=0,点C在y轴上,将△ 2020-06-14 …
如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平 2020-06-23 …
设A,B分别为双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)的左右顶点,双曲线的实轴长 2020-07-08 …
如图,一观测塔底座部分是四棱柱,现在从下底面A点修建钢筋扶梯,经过点M、N到点D′,再进入顶部的观 2020-07-20 …
已知开口向下的抛物线与x轴交于M、N两点(点N在点M的右侧),并且M和N两点的横坐标分别是方程的两 2020-07-20 …
(2000•甘肃)已知开口向下的抛物线y=ax2+bx+c与x轴交于M,N两点(点N在点M的右侧) 2020-07-21 …
如图,一次函数y=-12x+m(m>0)的图象与x轴、y轴分别交于点A、B,点C在线段OA上,点C的 2020-10-31 …
读图,完成下列问题:(1)根据经纬度描出下列各点:E(40°E,20°N)F(0°,20°N)G(3 2021-01-05 …