早教吧作业答案频道 -->数学-->
已知抛物线y2=4x,圆F:(x-1)2+y2=1,直线y=k(x-1)自上而下顺次与上述两曲线交于点A,B,C,D,则|AB||CD|的值是.
题目详情
已知抛物线y2=4x,圆F:(x-1)2+y2=1,直线y=k(x-1)自上而下顺次与上述两曲线交于点A,B,C,D,则|AB||CD|的值是___.
▼优质解答
答案和解析
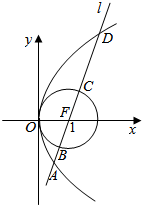 ∵y2=4x,焦点F(1,0),准线 l0:x=-1.
∵y2=4x,焦点F(1,0),准线 l0:x=-1.
由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1,
故答案为1.
 ∵y2=4x,焦点F(1,0),准线 l0:x=-1.
∵y2=4x,焦点F(1,0),准线 l0:x=-1.由定义得:|AF|=xA+1,
又∵|AF|=|AB|+1,∴|AB|=xA,
同理:|CD|=xD,
当l⊥x轴时,则xD=xA=1,∴|AB|•|CD|=1
当l:y=k(x-1)时,代入抛物线方程,得:k2x2-(2k2+4)x+k2=0,
∴xAxD=1,∴|AB|•|CD|=1
综上所述,|AB|•|CD|=1,
故答案为1.
看了 已知抛物线y2=4x,圆F:...的网友还看了以下:
已知,直线AB‖CD,直线AB与圆心O相切于点P,若圆心O半径为10cm,AB与CD之间的距离为1 2020-05-17 …
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于 2020-07-20 …
(2014•塘沽区二模)如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥C 2020-07-20 …
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交A 2020-07-21 …
又一道关于圆的问题圆O1与圆O2外切与P,AB、CD是两圆的外公切线,A、B、C、D为切点,内公切 2020-07-26 …
AB是圆O的直径,C是圆上一动点(不与A、B重合),过点C作CD⊥AB交圆O于D,交AB于F,∠O 2020-07-31 …
已知直线圆EM经过圆O的圆心,分别交圆O于B,C两点,直线EM与圆O相切于点A,CD垂直EM于点D 2020-07-31 …
已知A(1,1)是椭圆x^2/a^2+y^2/b^2(a>b>0)上一点F1,F2是椭圆的两焦点,且 2020-11-07 …
已知在圆O中,线段AB和CD将圆分成S1,S2,S3,S4四块,而且圆心O到AB和CD的距离分别为3 2020-11-10 …
匿名2008-11-04已知,半圆匿名2008-11-04已知,半圆的直径AB=6cm,CD是半圆上 2020-12-26 …