早教吧作业答案频道 -->数学-->
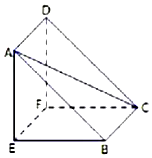
如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=7,四边形ABCD是正方形.(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑,判断四面体EABC是否为鳖
题目详情
如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=
,四边形ABCD是正方形.
(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑,判断四面体EABC是否为鳖臑,若是,写出其每一个面的直角,并证明;若不是,请说明理由.
(2)求四面体EABC的体积.
| 7 |

(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑,判断四面体EABC是否为鳖臑,若是,写出其每一个面的直角,并证明;若不是,请说明理由.
(2)求四面体EABC的体积.
▼优质解答
答案和解析
(1)∵AE⊥底面BCFE,EC,EB,BC都在底面BCFE上,
∴AE⊥EC,AE⊥EB,AE⊥BC,
∵四边形ABCD是正方形有,∴BC⊥AB,
∴BC⊥面ABE,又BE⊂面ABE,∴BC⊥BE,
∴四面体EABC是鳖臑.
(2)由(1)得AE是三棱锥A-BCE的高,
设正方形ABCD的边长为x,则AB=BC=x,BE=
=
,EC=
,
在Rt△BEC中,EC2=BE2+BC2,
即(
)2=x2+x2-1,解得x=2,
∴S△BCE=
×2×
=
,
∴四面体EABC的体积VA-BCE=
•AE•S△BCE=
×
=
.
∴AE⊥EC,AE⊥EB,AE⊥BC,

∵四边形ABCD是正方形有,∴BC⊥AB,
∴BC⊥面ABE,又BE⊂面ABE,∴BC⊥BE,
∴四面体EABC是鳖臑.
(2)由(1)得AE是三棱锥A-BCE的高,
设正方形ABCD的边长为x,则AB=BC=x,BE=
| AB2-AE2 |
| x2-1 |
| 7 |
在Rt△BEC中,EC2=BE2+BC2,
即(
| 7 |
∴S△BCE=
| 1 |
| 2 |
| 3 |
| 3 |
∴四面体EABC的体积VA-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 3 |
看了 如图所示为一名曰“堑堵”的几...的网友还看了以下:
EXCEL有没有什么公式能自动计算下列区域数值等于180?如何计算下面的数字结果?不是=B1+D1 2020-05-16 …
A、B、C、D、E,五个人如下排列:A在C前面6米,B在C后面8米,A在E前面2米,E在D前面7米 2020-07-03 …
求模运算d×e=1mod160,已知e=7,请问d=?这是加密的一个运算例子,鄙人数学不好,望指教 2020-07-07 …
SQL计算列的问题我要在数据库中加入计算列,比如有a,b,c三列,计算列D=(a+b+c)/3,然 2020-07-10 …
matlab中怎么计算x='-(a^2*c-b*d^2-a^2*e+c*d^2-2*a*c*d+2 2020-07-24 …
计算∫(上限+∞下限0)xe^(-x)/(1+e^(-x))^2其中过程是∫xe^(-x)dx/( 2020-07-31 …
在棱长为2的正方体ABCD-A'B'C'D'中,E是棱C'D'的中点,求过A.C,E,的截面EFG 2020-08-03 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …
已知向量a≠e,|e|=1,对任意t∈R,恒有|a-te|≥|a-e|,则(a,e皆为向量)A.a⊥ 2020-11-02 …
A、B、C、D、E五个人如下排列:A在C前面6米;B在C后面8米;A在E前面2米;E在D前面7米.请 2020-12-29 …