早教吧作业答案频道 -->数学-->
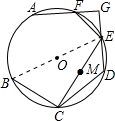
如图,BE是O的直径,点A,C,D,F都在O上,AE=CD,连接CE,M是CE的中点,延长DE到点G,使得EG=DE,并且交AF的延长线于点G,此时F恰为AG的中点.(1)若∠CDE=120°,CE=43,求O的周长.(2)求
题目详情
如图,BE是 O的直径,点A,C,D,F都在 O上,
=
,连接CE,M是CE的中点,延长DE到点G,使得EG=DE,并且交AF的延长线于点G,此时F恰为AG的中点.
(1)若∠CDE=120°,CE=4
,求 O的周长.
(2)求证:2FE=CE.
(3)试探索:在
上是否存在一点N,使得四边形NMEF是轴对称图形,并说明理由.
 |
| AE |
 |
| CD |

(1)若∠CDE=120°,CE=4
| 3 |
(2)求证:2FE=CE.
(3)试探索:在
 |
| AB |
▼优质解答
答案和解析
(1)如图1,连接OM,OC
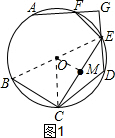
∵∠CDE=120°,
∴∠CBE=60°,
∴∠COE=120°,
∵M是CE的中点,
∴∠MOE=60°,∠OME=90°,
∵CE=4
,
∴EM=2
,
∴OE=4,
∴ O的周长为2π×OE=8π.
(2)如图2,连接AD,

∵F恰为AG的中点,EG=DE,
∴2EF=AD,
∵
=
,
∴
=
,
∴AD=CE,
∴2FE=CE.
(3)在
上存在一点N,使得四边形NMEF是轴对称图形,
理由如下:
如图3,连接FM,过点E作EN⊥FM,
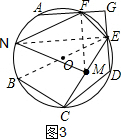
∵EF=EM,由(1)可得,
∴EN⊥FM,且平分FM,
∴在
上是存在一点N,使得四边形NMEF是轴对称图形.

∵∠CDE=120°,
∴∠CBE=60°,
∴∠COE=120°,
∵M是CE的中点,
∴∠MOE=60°,∠OME=90°,
∵CE=4
| 3 |
∴EM=2
| 3 |
∴OE=4,
∴ O的周长为2π×OE=8π.
(2)如图2,连接AD,

∵F恰为AG的中点,EG=DE,
∴2EF=AD,
∵
 |
| AE |
 |
| CD |
∴
 |
| AD |
 |
| CE |
∴AD=CE,
∴2FE=CE.
(3)在
 |
| AB |
理由如下:
如图3,连接FM,过点E作EN⊥FM,

∵EF=EM,由(1)可得,
∴EN⊥FM,且平分FM,
∴在
 |
| AB |
看了如图,BE是O的直径,点A,C...的网友还看了以下:
如图所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧, 2020-06-05 …
如图①,现有一张三角形ABC纸片,沿BC边上的高AE所在的直线翻折,使得点C与BC边上的点D重合. 2020-06-08 …
如图,矩形ABCD中,对角线AC=23,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的 2020-06-17 …
一道↖(^ω^)↗↖(^ω^)↗↖(^ω^)↗在△ABC中,∠BAC=90°,AB=AC,AE是过 2020-07-03 …
如图所示,在平面直角坐标系中,线段AB的端点A在y轴上,端点B在x轴上,BF平分∠ABO并与△AB 2020-07-22 …
如图1所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的异侧 2020-07-22 …
理解证明:如图1,∠MAN=90°,射线AE在这个角的内部,点B,C在∠MAN的边AM,AN上,且 2020-07-29 …
已知等边△ABC的顶点A在平面α上,B,C在的α同侧,D为BC中点,△ABC在α上的射影是以A为直 2020-07-30 …
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD 2020-11-02 …
如图1,△ABC中,角BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥ 2020-11-02 …