早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=2(1)求证:B1C∥平面A1BM(2)求证:平面AC1B1⊥平面A1BM.
题目详情
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=
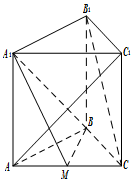
(1)求证:B1C∥平面A1BM
(2)求证:平面AC1B1⊥平面A1BM.
| 2 |

(1)求证:B1C∥平面A1BM
(2)求证:平面AC1B1⊥平面A1BM.
▼优质解答
答案和解析
证明:(1)连接AB1交A1B于O,连接OM.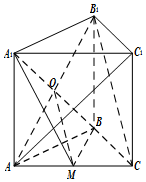
在△B1AC中,∵M,O分别为AC,AB1的中点,
∴OM∥B1C.
又∵OM⊂平面A1BM,B1C⊄平面A1BM,
∴B1C∥平面A1BM.
(2)∵侧棱AA1⊥底面ABC,BM⊂平面ABC,∴AA1⊥BM.
又∵M为棱AC中点,AB=BC,∴BM⊥AC.
∵AA1∩AC=A,∴BM⊥平面ACC1A1.
∴BM⊥AC1.
∵M为棱AC中点,AC=2,∴AM=1.
又∵AA1=
,∴在RT△ACC1和RT△A1AM中,
tan∠ACC1=tan∠A1MA=
,
∴∠ACC1=∠A1MA,
即∠ACC1+∠C1AC=∠A1MA+∠C1AC=90°,.
∴A1M⊥AC1.∵BM∩A1M=M,
∴AC1⊥平面A1BM.AC1⊂平面AC1B1
平面AC1B1⊥平面A1BM.

在△B1AC中,∵M,O分别为AC,AB1的中点,
∴OM∥B1C.
又∵OM⊂平面A1BM,B1C⊄平面A1BM,
∴B1C∥平面A1BM.
(2)∵侧棱AA1⊥底面ABC,BM⊂平面ABC,∴AA1⊥BM.
又∵M为棱AC中点,AB=BC,∴BM⊥AC.
∵AA1∩AC=A,∴BM⊥平面ACC1A1.
∴BM⊥AC1.
∵M为棱AC中点,AC=2,∴AM=1.
又∵AA1=
| 2 |
tan∠ACC1=tan∠A1MA=
| 2 |
∴∠ACC1=∠A1MA,
即∠ACC1+∠C1AC=∠A1MA+∠C1AC=90°,.
∴A1M⊥AC1.∵BM∩A1M=M,
∴AC1⊥平面A1BM.AC1⊂平面AC1B1
平面AC1B1⊥平面A1BM.
看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
求解几道不等式证明1.求证:x²>4x—5.2.求证:a的四次方+1≥a的三次方+a3.已知a>0 2020-04-27 …
证集合A={x x=2n+1 n属于Z}集合B={x x=4n+-1N属于Z}证明A=B虽然我懂先 2020-05-15 …
民事诉讼是解决建设工程纠纷的重要方式。其中民事诉讼的参与人不包括( )A.证人 B.第三人 C 2020-05-18 …
强制检查只适用于()。 A. 证人B. 被害人 C. 犯罪嫌疑人D. 见证人 2020-05-19 …
下列选项中,可以成为伪证罪的主体的是( )。A.证人B.鉴定人C.翻译人D.辩护人 2020-06-04 …
注册会计师依法执行审计业务出具的报告,具有( )效力。A.证明B.公证C.公示D.确定 2020-06-07 …
若m<0,n<0,且|m|>|n|,则(-m)+n的值一定是()a.证书b.负数c0 2020-07-09 …
英语翻译现在的问题是:A证(certificate)可以按你的要求显示,但是B证上只能体现伊朗的地 2020-07-21 …
设A,B是n阶矩阵,A与B相似且A适合A^2=A,证明B^2=B 2020-11-02 …
——“AEIOU”分析方法,其中“E”代表的含义是?在《远程学习导引》一书中,提到了一种深入分析具体 2020-12-05 …