早教吧作业答案频道 -->数学-->
在锐角△ABC中,角A、B、C所对的边分别是a、b、c,已知,且b=2,c=3,O为△ABC的外心,则=.
题目详情
在锐角△ABC中,角A、B、C所对的边分别是a、b、c,已知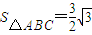 ,且b=2,c=3,O为△ABC的外心,则
,且b=2,c=3,O为△ABC的外心,则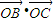 = .
= .
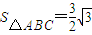 ,且b=2,c=3,O为△ABC的外心,则
,且b=2,c=3,O为△ABC的外心,则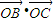 = .
= . ▼优质解答
答案和解析
【答案】 分析: 利用三角形的面积公式表示出三角形ABC的面积,使其等于已知的面积,把b和c的值代入求出sinA的值,由三角形ABC为锐角三角形,利用特殊角的三角函数值求出∠BAC的度数,进而求出cos∠BAC的值,由O为三角形的外心,根据同弧所对的圆心角等于圆周角的2倍,由∠BAC的度数求出∠BOC的度数,由b,c及cos∠BAC的值,利用余弦定理求出a的值,设三角形的外接圆半径为r,由a,sinA,利用正弦定理求出r的值,即为|OB|与|OC|的长,最后利用平面向量的数量积运算法则化简所求的式子,把各种的值代入即可求出值.
∵S △ABC =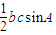 =
=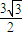 ,b=2,c=3,
,b=2,c=3,
∴sin∠BAC=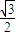 ,又△ABC为锐角三角形,
,又△ABC为锐角三角形,
∴∠BAC=60°,cos∠BAC= ,
,
∵O为△ABC的外心,
∴∠BOC=2∠BAC=120°,
∵b=2,c=3,cos∠BAC= ,
,
∴根据余弦定理得:a 2 =b 2 +c 2 -2bc•cos∠BAC=4+9-6=7,
解得:a=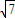 ,
,
由正弦定理可得:2r=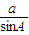 =
=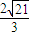 ,∴r=
,∴r=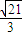 ,
,
则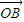 •
•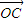 =|OB|•|OC|cos∠BOC=
=|OB|•|OC|cos∠BOC=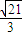 •
•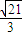 •cos120°=-
•cos120°=- .
.
故答案为:-
点评: 此题考查了三角形的面积公式,圆周角定理,正弦定理,以及平面向量的数量积运算法则,熟练掌握定理、公式及法则是解本题的关键.
∵S △ABC =
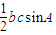 =
=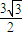 ,b=2,c=3,
,b=2,c=3,∴sin∠BAC=
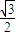 ,又△ABC为锐角三角形,
,又△ABC为锐角三角形,∴∠BAC=60°,cos∠BAC=
 ,
,∵O为△ABC的外心,
∴∠BOC=2∠BAC=120°,
∵b=2,c=3,cos∠BAC=
 ,
,∴根据余弦定理得:a 2 =b 2 +c 2 -2bc•cos∠BAC=4+9-6=7,
解得:a=
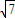 ,
,由正弦定理可得:2r=
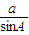 =
=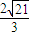 ,∴r=
,∴r=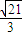 ,
,则
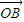 •
•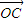 =|OB|•|OC|cos∠BOC=
=|OB|•|OC|cos∠BOC=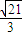 •
•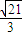 •cos120°=-
•cos120°=- .
.故答案为:-

点评: 此题考查了三角形的面积公式,圆周角定理,正弦定理,以及平面向量的数量积运算法则,熟练掌握定理、公式及法则是解本题的关键.
看了 在锐角△ABC中,角A、B、...的网友还看了以下:
已知向量a=(根号3,1)且向量b与a的夹角为30度,求b向量a,b满足:/a向量-b向量/=5a 2020-05-14 …
24 (a+b)/(c+d)=(√a^2+b^2)/√ (c^2+d^2)成立证明:(1)a/b= 2020-05-14 …
1.用描述法表示一元二次方程的全体,应是 ( )A.{x|ax2+bx+c=0,a,b,c∈R}; 2020-05-16 …
[20分][高一不等式]已知a,b,c∈R+,且a+b+c=1,求证1/a+1/b+1/c≥9已知 2020-06-10 …
设a,b,c∈R,证明a^2acc^23b(abc)≥0,并指出等号何时成立问题补充:证明:不妨设 2020-06-23 …
若a+b+c=1,且a、b、c为非负数,求证√a+√b+√c≤√3若a+b+c=1,且a、b、c为 2020-07-20 …
①如果a,b,c是有理数且abc≠0,计算代数式|a|a+|b|b+|c|c+|abc|abc的值 2020-07-29 …
三元一次方程组3a+2b-c=14且a+b-c=10且2a+3b-c=1.(1)若先消去a,得到关 2020-08-03 …
[已知a+b+c=6,且a,b,c>0,求证:(a+1/a)*(b+1/b)*(c+1/c)>=12 2020-10-30 …
关于数学向量的问题(1)若向量a,b,c,满足a+b+c=0,且a的模=3,b的模=1,c的模=4, 2020-12-18 …