早教吧作业答案频道 -->数学-->
已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.(1)求证:Q、H、K、P四点共圆;(2)求证:QT=TS.
题目详情
已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.
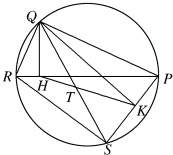
(1)求证:Q、H、K、P四点共圆;
(2)求证:QT=TS.

(1)求证:Q、H、K、P四点共圆;
(2)求证:QT=TS.
▼优质解答
答案和解析
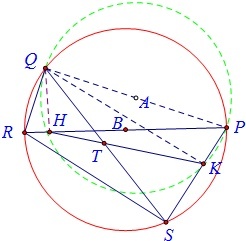 证明:(1)∵过点Q作PR、PS的垂线,垂足分别为点H、K,
证明:(1)∵过点Q作PR、PS的垂线,垂足分别为点H、K,
∴∠PHQ=∠PKQ=90°,
∴Q、H、K、P四点共圆;
(2)∵Q、H、K、P四点共圆,
∴∠HKS=
-∠HPQ=∠HQP,①
∵∠PSR=90°,PR为圆B的直径,
∴∠PQR=90°,∠QRH=∠HQP,②
由①②得,∠QSP=∠HKS,
∴△TSK为等腰三角形,ST=TK,
又∵∠SKQ=90°,
∴∠SQK=∠TKQ,即△TKQ为等腰三角形,QT=TK,
∴QT=TS.
 证明:(1)∵过点Q作PR、PS的垂线,垂足分别为点H、K,
证明:(1)∵过点Q作PR、PS的垂线,垂足分别为点H、K,∴∠PHQ=∠PKQ=90°,
∴Q、H、K、P四点共圆;
(2)∵Q、H、K、P四点共圆,
∴∠HKS=
| π |
| 2 |
∵∠PSR=90°,PR为圆B的直径,
∴∠PQR=90°,∠QRH=∠HQP,②
由①②得,∠QSP=∠HKS,
∴△TSK为等腰三角形,ST=TK,
又∵∠SKQ=90°,
∴∠SQK=∠TKQ,即△TKQ为等腰三角形,QT=TK,
∴QT=TS.
看了已知四边形PQRS是圆内接四边...的网友还看了以下:
(1)一个零件上,上面全是圆锥形,下面是圆柱形,他们的底面半径都是2厘米,高都是3厘米,这个零件的 2020-04-07 …
扇形OAB的圆心角为90°,四边形OCDE是边长为1的正方形如图,扇形AOB的圆心角为90°,四边 2020-05-17 …
已知,如图,点O是四边形ABCD的外接圆和内切圆的圆心,内切圆与四边形各边分别相切于点E、F、G、 2020-05-22 …
点O是四边形ABCD的外接圆和内切圆的圆心,内切圆与四边形各边分别相切于点E.F.G.H,求证四边 2020-05-22 …
已知圆O是△ABC的外接圆圆心O在这个三角形的高CD上(快的加分)已知圆O是△ABC的外接圆圆心O 2020-06-04 …
椭圆x2/a2+y2/b2+1的左右焦点分别为F1F2,短轴两个端点为AB且四边形F1AF2B是边 2020-06-11 …
如图.△ABC的三边分别切圆O于点D,E,F,AB=7,BC=8,AC=9如图,三角形ABC的三边 2020-06-15 …
为何晴朗之夜,月亮还是有圆缺之别?上玄月和下玄月分别是哪边缺哪边圆? 2020-06-30 …
数学证明题(圆)⊙O1和⊙2是等圆,P是O1O2的中点,过P作直线AD交⊙O1于A、B,交⊙O2于 2020-07-13 …
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半 2020-07-21 …