早教吧作业答案频道 -->数学-->
概念学习已知△ABC,点P为其内部一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.理解应用(1)判断
题目详情
概念学习
已知△ABC,点P为其内部一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.
理解应用
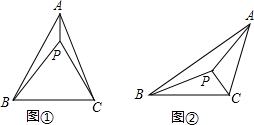
(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”
①内角分别为30、60、90的三角形存在等角点;___
②任意的三角形都存在等角点.___
(2)探究图①中∠BPC、∠ABC、∠ACP之间的数量关系,并说明理由.
解决问题
如图②,在△ABC中,∠A<∠B<∠C,若△ABC的三个内角的角平分线的交点P是该三角形的等角点.求该三角形三个内角的度数.
已知△ABC,点P为其内部一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形,其内角与△ABC的三个内角分别相等,那么就称点P为△ABC的等角点.
理解应用

(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”
①内角分别为30、60、90的三角形存在等角点;___
②任意的三角形都存在等角点.___
(2)探究图①中∠BPC、∠ABC、∠ACP之间的数量关系,并说明理由.
解决问题
如图②,在△ABC中,∠A<∠B<∠C,若△ABC的三个内角的角平分线的交点P是该三角形的等角点.求该三角形三个内角的度数.
▼优质解答
答案和解析
(1)①内角分别为30、60、90的三角形存在等角点是真命题;
②任意的三角形都存在等角点是假命题,如等边三角形不存在等角点;
故答案为:真,假;
(2)如图①,∵在△ABC中,∠BPC=∠ABP+∠BAC+∠ACP,∠BAC=∠PBC,
∴∠BPC=∠ABP+∠PBC+∠ACP=∠ABC+∠ACP;
(3)如图②,连接PB,PC
∵P为△ABC的角平分线的交点,
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∵P为△ABC的等角点,
∴∠PBC=∠A,∠BCP=∠ABC-2∠PBC=2∠A,∠ACB=∠BCP-4∠A,
又∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠A+4∠A=180°,
∴∠A=
,
∴该三角形三个内角的度数分别为
,
,
.
②任意的三角形都存在等角点是假命题,如等边三角形不存在等角点;
故答案为:真,假;
(2)如图①,∵在△ABC中,∠BPC=∠ABP+∠BAC+∠ACP,∠BAC=∠PBC,

∴∠BPC=∠ABP+∠PBC+∠ACP=∠ABC+∠ACP;
(3)如图②,连接PB,PC
∵P为△ABC的角平分线的交点,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵P为△ABC的等角点,
∴∠PBC=∠A,∠BCP=∠ABC-2∠PBC=2∠A,∠ACB=∠BCP-4∠A,
又∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠A+4∠A=180°,
∴∠A=
| 180° |
| 7 |
∴该三角形三个内角的度数分别为
| 180° |
| 7 |
| 360° |
| 7 |
| 720° |
| 7 |
看了概念学习已知△ABC,点P为其...的网友还看了以下:
如图,四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,直线PD与底面AB 2020-04-12 …
在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2根号2,角P 2020-05-16 …
已知:正方体ABCD-A'B'C'D'的棱成为a,P,Q,R,分别为棱AA',AB',BC'的中点 2020-05-16 …
在三棱锥P-ABC中,平面PAB⊥面ABC,PA⊥BC,△PAB是等边三角形,D是PB中点,求二面 2020-05-20 …
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是边长为2的正三角形,四边形ABC 2020-07-30 …
如图,△ABC中,∠A=90°,AB=4,AC=3,平面ABC外一点P在平面ABC内的射影是AB中 2020-07-30 …
(2008•天津)如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA= 2020-07-31 …
(2014•浙江模拟)如图,四棱锥P-ABCD,侧面PAD⊥底面ABCD,ABCD是直角梯形,△P 2020-07-31 …
在四棱锥P-ABCD中,底面ABCD为正方形,侧面PAD为正三角形,平面PAD⊥面ABCD(1)求 2020-07-31 …
(2012•浙江模拟)如图1所示,Rt△ABC中,BC=2,CA=3,点P在线段AB上,将△BPC 2020-08-02 …