早教吧作业答案频道 -->数学-->
已知∠ABC=90°,D是直线AB上的点,AD=BC.(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,
题目详情
已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
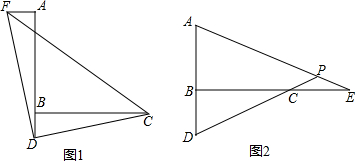
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.

▼优质解答
答案和解析
(1)∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
,
∴△FAD≌△DBC(SAS);
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形.
(2)如图2,作AF⊥AB于A,使AF=BD,连结DF,CF,
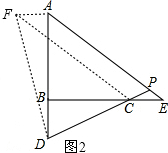
∴∠FAD=90°.
∵∠ABC=90°,
∴∠FAD=∠DBC=90°.
在△FAD和△DBC中,
,
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°.
∵∠APD=45°,
∴∠FCD=∠APD,
∴CF∥AE.
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,
∴CE=BD.
∴∠FAD=∠DBC,
在△FAD与△DBC中,
|
∴△FAD≌△DBC(SAS);
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形.
(2)如图2,作AF⊥AB于A,使AF=BD,连结DF,CF,

∴∠FAD=90°.
∵∠ABC=90°,
∴∠FAD=∠DBC=90°.
在△FAD和△DBC中,
|
∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.
∵∠BDC+∠BCD=90°,
∴∠ADF+∠BDC=90°,
∴∠FDC=90°,
∴∠FCD=45°.
∵∠APD=45°,
∴∠FCD=∠APD,
∴CF∥AE.
∵∠FAD=90°,∠ABC=90,
∴∠FAD=∠ABC,
∴AF∥BC.
∴四边形AECF是平行四边形,
∴AF=CE,
∴CE=BD.
看了已知∠ABC=90°,D是直线...的网友还看了以下:
串励电机,正转,反转的链接线路图.我有一个48V 600W 直流串励电动机,和48V的电源.但我不 2020-05-16 …
小明买了一只小灯泡,从包装盒上写的规格估算,用3节干电池对灯泡供电时通过小灯泡的电流约为0.8A. 2020-05-17 …
两台单相电压互感器接成(),又称为不完全星形接线。A:Y∕y接线B:D∕y接线C:V∕V接线D:Y∕ 2020-05-29 …
关于图中四大区域的叙述,正确的是()A.图一中C和D两大区域的分界线是400毫米等降水量线B.图二 2020-06-26 …
某同学用伏安法测量导体的电阻,现有量程为3V、内阻约为3kΩ的电压表和量程为0.6A、内阻约为0. 2020-06-30 …
(2012•盐城二模)供电公司检修人员用交流电表监控供电线路中强电流和高电压,使用的仪器是电流互感器 2020-11-12 …
为了监测变电站向外输电情况,要在变电站安装互感器,其接线如图所示.两变压器匝数分别为n1、n2和n3 2020-12-01 …
为了监测变电站向外输电的情况,要在变电站安装互感器,其接线如图所示,两变压器匝数分别为n1、n2和n 2020-12-01 …
现代程控电话交换机利用了什么进行接线?A.电磁继电器进行接线B.电子计算机技术进行接线C.手工操作进 2020-12-05 …
关于四大地理区域的叙述,正确的是()A.图①地区和图④地区的分界线是秦岭-淮河一线B.图②地区的农作 2020-12-08 …