早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,点E在边AB上(点E与点A、B不重合),过点E作FG⊥DE,FG与边BC相交于点F,与边DA的延长线相交于点G.(1)猜想BF、AG、AE的数量关系,并证明你所得到的结论;(2)如果
题目详情
如图,在正方形ABCD中,点E在边AB上(点E与点A、B不重合),过点E作FG⊥DE,FG与边BC相交于点F,与边DA的延长线相交于点G.
(1)猜想BF、AG、AE的数量关系,并证明你所得到的结论;
(2)如果正方形的边长为2,FG的长为
,求点A 到直线DE的距离.
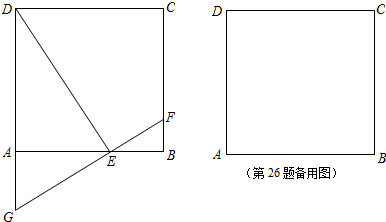
(1)猜想BF、AG、AE的数量关系,并证明你所得到的结论;
(2)如果正方形的边长为2,FG的长为
| 2 |
| 5 |

▼优质解答
答案和解析
(1)BF+AG=AE.理由如下: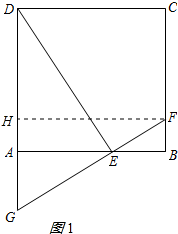
过点F作FH⊥DA,垂足为H,如图所示:
∵在正方形ABCD中,∠DAE=∠B=90°,
∴四边形ABFH是矩形,
∴FH=AB=DA.
∵BD⊥FG,
∴∠G=90°-∠ADE=∠DEA.
在△FHG和△DAE中,
,
∴△FHG≌△DAE(AAS).
∴GH=AE,即HA+AG=AE.
∵BF=HA,
∴BF+AG=AE.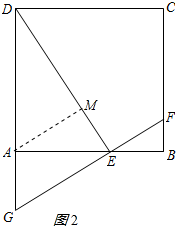
(2)过点A作AM⊥DE垂足为M.如图2所示:
由(1)得:△FHG≌△DAE,
∴DE=FG=
在Rt△ADE中,AE=
=
=
,
∵AE•AD=DE•AM,
∴AM=
=
即点A到直线DE的距离是
.

过点F作FH⊥DA,垂足为H,如图所示:
∵在正方形ABCD中,∠DAE=∠B=90°,
∴四边形ABFH是矩形,
∴FH=AB=DA.
∵BD⊥FG,
∴∠G=90°-∠ADE=∠DEA.
在△FHG和△DAE中,
|
∴△FHG≌△DAE(AAS).
∴GH=AE,即HA+AG=AE.
∵BF=HA,
∴BF+AG=AE.

(2)过点A作AM⊥DE垂足为M.如图2所示:
由(1)得:△FHG≌△DAE,
∴DE=FG=
| 5 |
| 2 |
在Rt△ADE中,AE=
| DE2-AD2 |
(
|
| 3 |
| 2 |
∵AE•AD=DE•AM,
∴AM=
| AE•AD |
| DE |
| 6 |
| 5 |
即点A到直线DE的距离是
| 6 |
| 5 |
看了如图,在正方形ABCD中,点E...的网友还看了以下:
在正方形ABCD各边上截取AE=BF=CG=DH,连结AF、BG、CH、DE,依次相交于A`B`C 2020-05-15 …
罗伯特森的关于生物膜模型的结构:所以的生物膜都由蛋白质 — 脂质 — 蛋白质三层结构构成,电镜下看 2020-05-17 …
对一棵二叉树的中序遍历序列中,根结点右边的结点属于()。A.左子树上的叶子结点B.右子树上的所有结 2020-05-23 …
如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重 2020-06-12 …
初一几个数学问题1、已知:在△ABC中,a、b、c为三边,且a²+b²+c²-ab-ac-bc=0 2020-07-03 …
如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于 2020-07-09 …
如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45 2020-07-09 …
如图,点E、F分别是平行四边形ABCD中AB、CD边延长线上的点,连结EF分别交AD、BC边于M、 2020-07-22 …
在RT三角形ABC中,∠C=90度,∠B=30度,斜边AB的垂直平分线DE交AB边于点D,交BC于 2020-07-30 …
如图,已知等腰三角形ABC的直角边AC=BC=a,等腰直角三角形BED的指教边BE=DE=b,且a小 2020-12-07 …