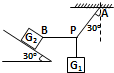
如图所示，重力为G1=9N的砝码悬挂在绳PA和PB的结点上，PA偏离竖直方向30°角，PB沿水平方向且连在重力为G2=100N的木块上，木块静止于倾角为30°的斜面上，（3=1.73，计算结果保留2位小数）求

Question

如图所示，重力为G₁=9N的砝码悬挂在绳PA和PB的结点上，PA偏离竖直方向30°角，PB沿水平方向且连在重力为G₂=100N的木块上，木块静止于倾角为30°的斜面上，（√(3)=1.73，计算结果保留2位小数）求：

（1）PA绳上的拉力；
（2）木块与斜面间的摩擦力；
（3）木块所受斜面的弹力．

Answer 1

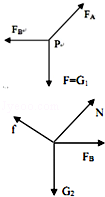（1）对结点P受力分析，由平衡条件得：
F_A=(G1)/(cos30°)=(9)/((√(3))/(2))N=6√(3)=10.38N    
（2）对结点P受力分析，由平衡条件得：
F_B=G₁tan30°=9×(√(3))/(3)=3√(3)N        
对木块G₂，由平衡条件可得：
平行斜面方向：f=G₂sin30°+F_Bcos30°    
解得：f=54.50N           
（3）对木块G₂，由平衡条件可得：
垂直斜面方向：F_N+F_Bsin30°=G₂ cos30°   
解得：F_N=48.5√(3)N=83.91N 
答：（1）PA绳上的拉力为10.38N
（2）木块与斜面间的摩擦力是54.50N；
（3）木块所受斜面的弹力是83.91N．