定义平面上一点P到曲线C的距离为点P到曲线C上所有点距离的最小值,那么平面内到定圆的距离与到定点A的距离相等的点的轨迹不可能是()A.圆B.椭圆C.双曲线的一支D.直线
定义平面上一点P到曲线C的距离为点P到曲线C上所有点距离的最小值,那么平面内到定圆的距离与到定点A的距离相等的点的轨迹不可能是( )
A. 圆
B. 椭圆
C. 双曲线的一支
D. 直线
 排除法:设动点为Q,
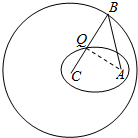
排除法:设动点为Q,1.当点A在圆内不与圆心C重合,连接CQ并延长,交于圆上一点B,由题意知QB=QA,又QB+QC=R,所以QA+QC=R,即Q的轨迹为一椭圆;如图.
2.如果是点A在圆C外,由QC-R=QA,得QC-QA=R,为一定值,即Q的轨迹为双曲线的一支;
3.当点A与圆心C重合,要使QB=QA,则Q必然在与圆C的同心圆,即Q的轨迹为一圆;
故选D.
求面积计算公式:空间一点到空间一圆上两点间弧所形成区域的面积求面积:空间一点到空间一圆上两点间弧所 2020-05-16 …
如图1-18所示,有一个圆柱,它的高等于12厘米,地面半径等于3厘米.在圆柱下地面的A点有一只蚂蚁 2020-06-02 …
写出由下列条件确定的曲线所满足的微分方程曲线上任一点的切线介于两坐标轴间的部分被切点等分曲线上任一 2020-06-21 …
这个世界真的没有一尘不变的事情?更没有一个人会永远在原点等你?所以,即使你跌到了,你也要豪迈的笑? 2020-06-26 …
下列表述正确的是()A.三点确定一个圆B.等弧所对的圆周角相等C.等弦所对的圆周角相等D.相等的圆 2020-07-13 …
在ABC中,AB=AC,边BC的中点为D.所作的等边DEF的边EF与BC平行吗三角形ABC,AB= 2020-07-22 …
圆的概念在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆,如图1所示 2020-07-31 …
下列命题中,假命题是()A.任意三点确定一个圆B.等弧所对的圆周角相等C.直径所对的圆周角是直角D 2020-07-31 …
在判断打点计时器所打纸带是否做匀速直线运动时,以下说法(不)能作为判断依据A纸带上相邻两点的间隔均 2020-08-02 …
等边三角形、全等三角形de初中题两个等边三角形有一个公共顶点,连接两个等边三角形的所有顶点,问一共 2020-08-02 …