早教吧作业答案频道 -->数学-->
对于函数y=f(x),若其定义域内存在不同实数x1,x2,使得xif(xi)=1(i=1,2)成立,则称函数f(x)具有性质P,若函数f(x)=exa具有性质P,则实数a的取值范围为.
题目详情
对于函数y=f(x),若其定义域内存在不同实数x1,x2,使得xif(xi)=1(i=1,2)成立,则称函数f(x)具有性质P,若函数f(x)=
具有性质P,则实数a的取值范围为___.
| ex |
| a |
▼优质解答
答案和解析
由题意知:若f(x)具有性质P,
则在定义域内xf(x)=1有两个不同的实数根,
∵f(x)=
,∴x•
=1,
即方程xex=a在R上有两个不同的实数根,
设g(x)=xex,则g′(x)=ex+xex=(1+x)ex,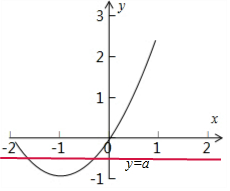
由g′(x)=0得,x=-1,
∴g(x)在(-∞,-1)上递减,在(-1,+∞)上递增,
∴当x=-1时,g(x)取到最小值是g(-1)=-
,
∵x<0,g(x)<0、x>0,g(x)>0,
∴当方程xex=a在R上有两个不同的实数根时,
即函数g(x)与y=a的图象有两个交点,
由图得-
<a<0,
∴实数a的取值范围为(-
,0),
故答案为:(-
,0).
则在定义域内xf(x)=1有两个不同的实数根,
∵f(x)=
| ex |
| a |
| ex |
| a |
即方程xex=a在R上有两个不同的实数根,
设g(x)=xex,则g′(x)=ex+xex=(1+x)ex,

由g′(x)=0得,x=-1,
∴g(x)在(-∞,-1)上递减,在(-1,+∞)上递增,
∴当x=-1时,g(x)取到最小值是g(-1)=-
| 1 |
| e |
∵x<0,g(x)<0、x>0,g(x)>0,
∴当方程xex=a在R上有两个不同的实数根时,
即函数g(x)与y=a的图象有两个交点,
由图得-
| 1 |
| e |
∴实数a的取值范围为(-
| 1 |
| e |
故答案为:(-
| 1 |
| e |
看了对于函数y=f(x),若其定义...的网友还看了以下:
请问∑上面是n下面是i=1,∑P(Xi)=1是什么意思?还有cloga是什么意思?H(XI)=cl 2020-05-15 …
在概率论中,为什么(n-1)S^2/ó^2是自由度为n-1的卡方分布?∑(xi-u)^2/σ^2∽ 2020-06-16 …
设X1,X2,…Xn为总体N(μ,σ2)的一个样本,已知σ2=Cn−1i=1(Xi+1-Xi)2为 2020-07-16 …
用一种粒子群优化算法和一种遗传算法解决下面优化问题minf(x)=∑(i=1)^n▒[xi^2-1 2020-07-23 …
数理统计问题总体X~N(u,σ^2),X1,X2,X3,Xn是来自X的一个样本,C∑X(i+1)-X 2020-10-31 …
某种产品广告的支出x与销售收入y(单位:万元)之间有下列所示的对应数据及统计数据.广告支出x/万元1 2020-10-31 …
某商店经营一批进价为每件4元的商品,在市场调查时得到,此商品的销售单价x与日销售量y之间的一组数据满 2020-11-01 …
在厄尔尼诺现象中,经观测,某昆虫的产卵数y与温度x有关,现将收集到的温度xi和产卵数yi(i=1,2 2020-11-01 …
(2012•东莞二模)设f(x)是定义在[a,b]上的函数,用分点T:a=x0<x1<…<xi-1< 2020-11-12 …
请认真阅读下列程序框图:已知程序框图xi=f(xi-1)中的函数关系式为f(x)=4x-2x+1,程 2021-01-15 …