早教吧作业答案频道 -->数学-->
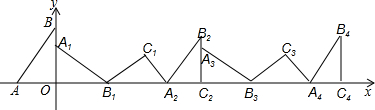
在平面直角坐标系中,按如图方式,沿x轴将△ABO绕它的顶点顺时针旋转,使它的顶点依次落在x轴上,如此下去…若点A(-3,0),B(0,4),请回答下列问题:(1)分别写出点A1,A3的坐标
题目详情
在平面直角坐标系中,按如图方式,沿x轴将△ABO绕它的顶点顺时针旋转,使它的顶点依次落在x轴上,如此下去…若点A(-3,0),B(0,4),请回答下列问题:
(1)分别写出点A1,A3的坐标,并用n表示点A2n-1的坐标;
(2)若点Am的坐标为(597,0),试求m的值.
(1)分别写出点A1,A3的坐标,并用n表示点A2n-1的坐标;
(2)若点Am的坐标为(597,0),试求m的值.

▼优质解答
答案和解析
(1)如图所示:∵点A(-3,0),B(0,4),
∴AO=3,BO=4,
∴AB=5,
则OA=OA1=3,故A1的坐标为:(0,3),
由题意可得:OB1=4,A2B1=5,A2C2=3,
故A3的坐标为:(12,3),
∵A2n-1是连续奇数的坐标,则其横坐标是12的倍数,纵坐标为3,故A2n-1[12(n-1),3];
(2)由题意可得:每3次三角形旋转一周,则移动距离为12,则A 2 (9,0),A4(21,0),A6(33,0),…
∵597÷12=49…9,
∴三角形从A2开始向右旋转49周,即可得到Am,且m是连续的偶数,即m是连续的第50个偶数.
故m的值为:50.
∴AO=3,BO=4,
∴AB=5,
则OA=OA1=3,故A1的坐标为:(0,3),
由题意可得:OB1=4,A2B1=5,A2C2=3,
故A3的坐标为:(12,3),
∵A2n-1是连续奇数的坐标,则其横坐标是12的倍数,纵坐标为3,故A2n-1[12(n-1),3];
(2)由题意可得:每3次三角形旋转一周,则移动距离为12,则A 2 (9,0),A4(21,0),A6(33,0),…
∵597÷12=49…9,
∴三角形从A2开始向右旋转49周,即可得到Am,且m是连续的偶数,即m是连续的第50个偶数.
故m的值为:50.
看了在平面直角坐标系中,按如图方式...的网友还看了以下:
A、B、C三人分别拿一只水桶到同一商店打水,他们打水所需的时间为3分钟、2分钟和4分钟.若按A-B 2020-04-11 …
若要求生产时间最短,应采取的工序间移动方式为( )。A.顺序移动方式 B.平行移动方式C.平行顺序 2020-05-21 …
如图(1),P是正方形ABCD内一点,将△PBC绕点B按顺时针方向旋转后与△EBA重合.(1)若P 2020-07-21 …
关于锐角三角函数.a为锐角,若tana=0.2,则a=?若cosa=0.5127,则a=a为锐角, 2020-07-30 …
斜三角形三角函数△ABC中,若∠A,∠B,∠C顺序成等差数列,则cos平方A+cos平方C的取值范 2020-08-02 …
如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜: 2020-10-29 …
数学小问题。。A.B两个港口相距300千米。若甲船顺水自A驶向B,乙船同时自B逆水驶向A,两船在C出 2020-11-04 …
某加工件的批量n=4件,需顺序经过4道工序加工,各工序的单件作业时间分别为:t2=5分,t4=15分 2020-12-01 …
求平行顺序移动计算中较大,较小的判别方式原题为:若工艺顺序及单间工序时间为:t1=10min,t2= 2020-12-01 …
一个正方行的边长是a米,100个这样的正方形顺次拼成一个长方形,这个长方形的周长是多少米?(要方程) 2020-12-17 …