早教吧作业答案频道 -->数学-->
如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.(1)求证:△DCA≌△EAC;(2)只需添加一个条件,即,可使四边形ABCD为矩形.请加以证明.
题目详情
如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.
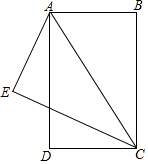
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即___,可使四边形ABCD为矩形.请加以证明.

(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即___,可使四边形ABCD为矩形.请加以证明.
▼优质解答
答案和解析
(1)证明:在△DCA和△EAC中,
,
∴△DCA≌△EAC(SSS);
(2) 添加AD=BC,可使四边形ABCD为矩形;理由如下:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,
∵CE⊥AE,
∴∠E=90°,
由(1)得:△DCA≌△EAC,
∴∠D=∠E=90°,
∴四边形ABCD为矩形;
故答案为:AD=BC(答案不唯一).
|
∴△DCA≌△EAC(SSS);
(2) 添加AD=BC,可使四边形ABCD为矩形;理由如下:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,
∵CE⊥AE,
∴∠E=90°,
由(1)得:△DCA≌△EAC,
∴∠D=∠E=90°,
∴四边形ABCD为矩形;
故答案为:AD=BC(答案不唯一).
看了如图,已知BA=AE=DC,A...的网友还看了以下:
三角形abc中,d,e是bc,ac上的点,ad,be交于f若已知bd:dc=2:3,ae:ec=1 2020-05-15 …
7.已知方阵A与对角阵B=相似,则A2=()A.-64EB.-EC.4ED.64E对角阵B是三阶矩 2020-06-18 …
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥A 2020-06-27 …
(2013•舟山)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB 2020-07-19 …
如图O中,半径OD⊥弦AB于点C,连结AO并延长交O于点E,连结EC,若AB=8,CD=2,则EC 2020-07-19 …
在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,C 2020-07-21 …
直角梯形ABCD中,AB//CD,∠BCD=90度,BC=CD=√2,AD=BD,EC⊥底面ABC 2020-07-30 …
1道简单证明题在平行四边形ABCD中,已知向量AB=a,向量AD=b,向量AE=2向量EC,向量B 2020-08-01 …
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果∠ECD=55°,那么下列说法错误的是 2020-08-03 …
数学向量1,A,B,C,D为平面上4个互异点,且满足(向量DB+DC-2DA)点乘(AB-AC)=0 2020-11-02 …