早教吧作业答案频道 -->数学-->
在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,CD=2,AC=EC=5.(1)求证:平面EBC⊥平面EBD;(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT
题目详情
在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形.AB∥DC,AB=AD=1,CD=2,AC=EC=
.
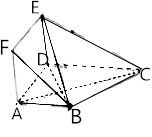
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;不存在,请说明理由.
| 5 |

(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;不存在,请说明理由.
▼优质解答
答案和解析
证明:(1)∵AD=1,CD=2,AC=
,
∴AD2+CD2=AC2,∴△ADC为直角三角形,且AD⊥DC,
同理∵ED=1,CD=2,EC=
,
∴ED2+CD2=EC2,∴△EDC为直角三角形,且ED⊥DC,
又四边形ADEF是正方形,∴AD⊥DE,
又∵AB∥DC,∴DA⊥AB,
在梯形ABCD中,过点B作BH⊥CD于H,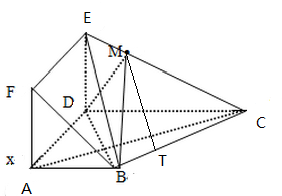
故四边形ABHD是正方形,∴∠ADB=45°,
在△BCH中,BH=CH=1,∠BCH=45°,BC=
,
∴在∠BDC=45°,∴∠DBC=90°,∴BC⊥BD,
∵ED⊥AD,ED⊥DC,AD∩DC=D,
∴ED⊥平面ABCD,
又∵BC⊂平面ABCD,∴ED⊥BC,
∵BD∩ED=D,BD⊂平面EBD,ED⊂平面EBD,
∴BC⊥平面EBD,BC⊂平面EBC,
∴平面EBC⊥平面EBD.
(2)∵M为线段EC上一点,且3EM=EC,
在线段BC上取一点T,使3BT=TC,则MT∥平面BDE.
理由如下:
∵M为线段EC上一点,且3EM=EC,T为BC上一点,3BT=TC,
∴MT∥BE,∵BE⊂平面BDE,MT⊄平面BDE,
∴MT∥平面BDE.
| 5 |
∴AD2+CD2=AC2,∴△ADC为直角三角形,且AD⊥DC,
同理∵ED=1,CD=2,EC=
| 5 |
∴ED2+CD2=EC2,∴△EDC为直角三角形,且ED⊥DC,
又四边形ADEF是正方形,∴AD⊥DE,
又∵AB∥DC,∴DA⊥AB,
在梯形ABCD中,过点B作BH⊥CD于H,

故四边形ABHD是正方形,∴∠ADB=45°,
在△BCH中,BH=CH=1,∠BCH=45°,BC=
| 2 |
∴在∠BDC=45°,∴∠DBC=90°,∴BC⊥BD,
∵ED⊥AD,ED⊥DC,AD∩DC=D,
∴ED⊥平面ABCD,
又∵BC⊂平面ABCD,∴ED⊥BC,
∵BD∩ED=D,BD⊂平面EBD,ED⊂平面EBD,
∴BC⊥平面EBD,BC⊂平面EBC,
∴平面EBC⊥平面EBD.
(2)∵M为线段EC上一点,且3EM=EC,
在线段BC上取一点T,使3BT=TC,则MT∥平面BDE.
理由如下:
∵M为线段EC上一点,且3EM=EC,T为BC上一点,3BT=TC,
∴MT∥BE,∵BE⊂平面BDE,MT⊄平面BDE,
∴MT∥平面BDE.
看了 在多面体ABCDEF中,底面...的网友还看了以下:
设不等式组x+y≤1x≥0y≥0,表示的平面区域为M,在圆x∧2+y∧2=r∧2(r>0)设不等式 2020-04-12 …
1/2{1/2[1/2(1/2y-3)-3]-3}=17x-1/0.024=1-0.2x/0.08 2020-04-27 …
(1)1/1*2+1/2*3+.+1/2009*2010(2)1/2*4+1/4*6+.+1/20 2020-05-17 …
(1)数列{an}是以1为首项,以2为公比的等比数列,求S=a1C0n+a2C1n+a3C2n+… 2020-07-09 …
(1/2+1/3+1/4+...1/2013)X(1+1/2+1/3+1/4+...1/2012) 2020-07-14 …
设R^3中的一组基ξ1=(1,-2,1)T,ξ2=(0,1,1)T,ξ3=(3,2,1)T,向量α在 2020-11-02 …
初一一道数学找规律的题急用1.将1,-1/2,1/3,-1/4,1/5,-1/6,.按一定的规律排列 2020-11-03 …
求一道预备班数学期中考试的答案小明在做题时发现了一个规律:1*2/1=1-2/1,2*3/1=2/1 2020-11-05 …
观察下列等式①1/√2+1=√2-1/(√2+1)(√2-1)=-1+√2②1/√3+√2=√3-√ 2020-12-07 …
豌豆叶肉细胞、噬菌体、大肠杆菌、烟草花叶病毒中的核酸、含有的碱基种类分别是()A.1、1、1、1;4 2020-12-08 …