如图，在正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G1，G2，G3三点重合于点G，这样，下列五个结论：①SG⊥平面EFG；②SD⊥平面

Question

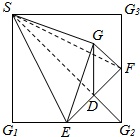
如图，在正方形SG₁G₂G₃中，E，F分别是G₁G₂，G₂G₃的中点，D是EF的中点，现沿SE，SF及EF把这个正方形折成一个几何体，使G₁，G₂，G₃三点重合于点G，这样，下列五个结论：①SG⊥平面EFG；②SD⊥平面EFG；③GF⊥平面SEF；④EF⊥平面GSD；⑤GD⊥平面SEF．
其中正确的是___（填序号）．

Answer 1

证明：∵在折叠过程中，始终有SG1⊥G₁E，SG₃⊥G₃F，
即SG⊥GE，SG⊥GF，
∴SG⊥平面EFG．
故答案为：①．