如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是(
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )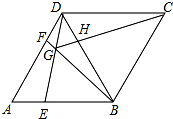
A. 只有①②
B. ①②③
C. 只有②③
D. 只有①③
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本小题正确;
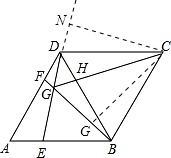
②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=
| 1 |
| 2 |
| ||
| 2 |
∴S四边形CMGN=2S△CMG=2×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
③过点F作FP∥AE于P点.
∵AF=2FD,
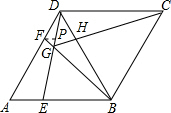
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即BG=6GF,故本小题正确.
综上所述,正确的结论有①③.
故选D.
A列为百分比,B列为分值,我要用IF公式求,如果A列数值小于1,B=A*所占分值,如果A列大于1, 2020-04-25 …
如果a的立方根与b的立方根的和的绝对值等于a的立方根的绝对值减去(b的立方根与ab的乘积)且不等于 2020-05-13 …
若b分之a大于0,则下列说法正确的是,现在就要!若b分之a大于0,则下列说法正确的是:A、a大于0 2020-05-14 …
用适当的符号表示下列各题中集合A,B之间的关系:(1)A={xlx=2n,n属于N},B={xlx 2020-05-16 …
excel表格中,E列为60,A列为10,B列为50,C列20,D列为40,如何设值E列既等于A列 2020-06-12 …
若(-ab)的2005次方大于0,则下列正确的是:()若(-ab)的2005次方大于0,则下列正确 2020-07-09 …
设Sn为数列{an}的前n项和,对任意的n属于N*都有Sn=(m+1)-man(m为常数且m大于0 2020-08-01 …
设4阶矩阵A=(a,b,c,d),B=(e,b,c,d),其中a,b,c,d,e均为4维列向量,且 2020-08-03 …
1.下列句子中的“于”是表示被动的是(D)A.移其民于河东B西取由余于戎C.吾长见于大方之家D.夫物 2020-11-07 …
高二数学问题2已知数列{a[n]}中,a1=1,a2=r(r大于0)且数列{a[n]*a[n+1]} 2020-11-29 …