早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动
题目详情
如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动,连结PQ、PB,设△PBQ的面积为S,运动时间为t秒,S关于t的大致函数图象如图所示.
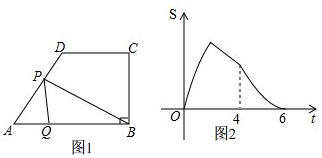
(1)求DC的长;
(2)求出图2中第二段的解析式;
(3)当t为何值时,△PBQ的面积5?

(1)求DC的长;
(2)求出图2中第二段的解析式;
(3)当t为何值时,△PBQ的面积5?
▼优质解答
答案和解析
(1)∵AB=2CD,
∴AD+CD+BC>2AB,
∴点Q先到达终点,由图2,两个点停止时,用了6秒,
∵点Q的运动速度是每秒1个单位,
∴AB=6,
∴DC=3;
(2)如图1,2,
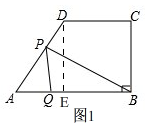
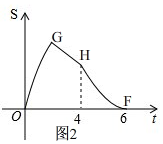
由图2,点P运动4秒时,刚好到达点C,
∴AD+CD=2×4=8,
由(1)知,CD=3,
∴AD=5,
过点D作DE⊥AB于E,
∴BC=DE,
在Rt△ADE中,AE=AB-CD=3,根据勾股定理得,DE=4,
∴BC=4,
∴点P运动5÷2=
秒时,点P到达点D的位置,AQ=
,BQ=AB-AQ=
,
∴S=
BQ•DE=
×
×4=17,
∴G(
,7),
点P运动到点C时,运动时间为4,BQ=AB-AQ=2,
∴S=
BQ×BC=
×2×4=4,
∴H(4,4)
图2中第二段函数是高为BC=4,底BQ逐渐减少,
∴第二段函数是一段线段,
此线段过点G(
,7),H(4,4),
∴图2中第二段的解析式为S=-2t+12(
≤t≤4);
(3)由(2)知,点P在AD上和CD上时,△PBQ=5,
当点P在AD上时,如图3,
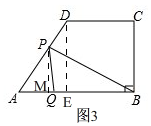
过点D作DE⊥AB于E,过点P作PM⊥AB于M,
在Rt△ADE中,sin∠DAE=
=
,
在Rt△APM中,PM=AP•sin∠DAE=2t×
=
,
BQ=AB-AQ=6-t,
∴S=
BQ•PM=
(6-t)×
=5,
∴t=
(舍)或t=
当点P在CD上时,由(2)知,S=-2t+12,
∴-2t+12=5,
∴t=
;
∴AD+CD+BC>2AB,
∴点Q先到达终点,由图2,两个点停止时,用了6秒,
∵点Q的运动速度是每秒1个单位,
∴AB=6,
∴DC=3;
(2)如图1,2,


由图2,点P运动4秒时,刚好到达点C,
∴AD+CD=2×4=8,
由(1)知,CD=3,
∴AD=5,
过点D作DE⊥AB于E,
∴BC=DE,
在Rt△ADE中,AE=AB-CD=3,根据勾股定理得,DE=4,
∴BC=4,
∴点P运动5÷2=
| 5 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴G(
| 5 |
| 2 |
点P运动到点C时,运动时间为4,BQ=AB-AQ=2,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴H(4,4)
图2中第二段函数是高为BC=4,底BQ逐渐减少,
∴第二段函数是一段线段,
此线段过点G(
| 5 |
| 2 |
∴图2中第二段的解析式为S=-2t+12(
| 5 |
| 2 |
(3)由(2)知,点P在AD上和CD上时,△PBQ=5,
当点P在AD上时,如图3,

过点D作DE⊥AB于E,过点P作PM⊥AB于M,
在Rt△ADE中,sin∠DAE=
| DE |
| AD |
| 4 |
| 5 |
在Rt△APM中,PM=AP•sin∠DAE=2t×
| 4 |
| 5 |
| 8t |
| 5 |
BQ=AB-AQ=6-t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 8t |
| 5 |
∴t=
6-
| ||
| 2 |
6-
| ||
| 2 |
当点P在CD上时,由(2)知,S=-2t+12,
∴-2t+12=5,
∴t=
| 7 |
| 2 |
看了 如图,已知四边形ABCD中,...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
几道关于三角函数的题,1.在Rt△ABC中,∠C=90°﹙1﹚已知a=35,c=35根号2,求∠A 2020-07-21 …
1命题若a=x/4则tana=1的逆否命题是2设集合A=(a,b)b=(b,c,d)则AUB=3若 2020-08-02 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …