早教吧作业答案频道 -->数学-->
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.(1)求抛物线的解析式;(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m
题目详情
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.
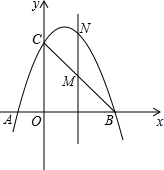
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由.
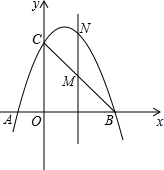
(1)求抛物线的解析式;
(2)点M是线段BC上的点(不与B、C重合),过M作NM∥y轴交抛物线于N,若点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点m,使△BNC的面积最大?若存在,求m的值和△BNC的面积;若不存在,说明理由.
▼优质解答
答案和解析
(1)∵抛物线经过点A(-1,0),B(3,0),C(0,3)三点,
∴设抛物线的解析式为:y=a(x+1)(x-3),
把C(0,3)代入得:3=a(0+1)(0-3),
a=-1,
∴y抛物线的解析式:y=-x2+2x+3;
(2)设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得:
,
解得:
,
∴直线BC的解析式为y=-x+3,
∴M(m,-m+3),
又∵MN⊥x轴,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3);
(3)存在,
S△BNC=S△CMN+S△MNB=
|MN|•|OB|,
∴当|MN|最大时,△BNC的面积最大,
MN=-m2+3m=-(m-
)2+
,
当m=
时,MN的有最大值为
,
所以当m=
时,△BNC的面积最大为
×
×3=
.
∴设抛物线的解析式为:y=a(x+1)(x-3),
把C(0,3)代入得:3=a(0+1)(0-3),
a=-1,
∴y抛物线的解析式:y=-x2+2x+3;
(2)设直线BC的解析式为:y=kx+b,
把B(3,0),C(0,3)代入得:
|
解得:
|
∴直线BC的解析式为y=-x+3,
∴M(m,-m+3),
又∵MN⊥x轴,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3);
(3)存在,
S△BNC=S△CMN+S△MNB=
| 1 |
| 2 |
∴当|MN|最大时,△BNC的面积最大,
MN=-m2+3m=-(m-
| 3 |
| 2 |
| 9 |
| 4 |
当m=
| 3 |
| 2 |
| 9 |
| 4 |
所以当m=
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
看了如图,已知抛物线经过点A(-1...的网友还看了以下:
已知集合A={x|x=3n+1,n∈Z},B={x|x=3n+2,n∈Z},M={x|x=6n+3 2020-04-05 …
一个尺规作图的问题在平面中有两条非平行的直线A、B,若要在直线B上截取一点M,使点M到直线A的距离 2020-04-26 …
如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足(1)填空:a=,b=;( 2020-06-13 …
有难度M{A,B,C}==(A+B+C)/3m{A,B,C}=A(A为三数中最小的一个)则若M{A 2020-06-13 …
如何确定一个关系模式的规范化程度F={B->C,(M,T)->B,(M,C)->T,(M,A)-> 2020-06-28 …
把自然数A和B分解质因数得到A=2乘以5乘以7乘以M,B=3乘以5乘以M,如果A和B的最小公倍数是 2020-07-20 …
张强同学设计了如下问题:定义:把形如a+b√m,a-b√m(a,b为有理数且b≠0,m为正整数且开 2020-07-30 …
初三数学题~如果a.b都是质数,且a^2-13a+m=0,b^2-13b+m=0,那么a/b+b/a 2020-10-30 …
用※定义新运算:对于任意有理数a,b,都有a※b=b的平方+1.例如7※4=4的平方+1=17,那么 2020-12-31 …
求神人帮忙解下题√=根号张强同学设计了如下问题:定义:把形如a+b√m,a-b√m(a、b为有理数且 2021-01-20 …