早教吧作业答案频道 -->数学-->
如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.(1)求证:DC是⊙O的切线;(2)若AE=1,ED=3,求⊙O的半径.
题目详情
如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
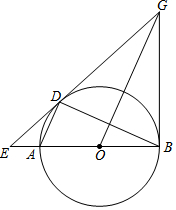
(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.
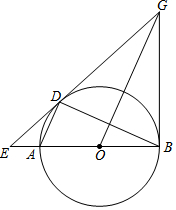
(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.
▼优质解答
答案和解析
(1)证明:连结DO.
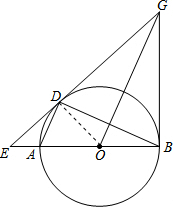
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中
∵OD=OB,OC=OC,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO.
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,
又∵点D在⊙O上,
∴CD是⊙O的切线;
(2)设⊙O的半径为R,则OD=R,OE=R+1,
∵CD是⊙O的切线,
∴∠EDO=90°,
∴ED2+OD2=OE2,
∴32+R2=(R+1)2,
解得R=2,
∴⊙O的半径为2.

∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中
∵OD=OB,OC=OC,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO.
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,
又∵点D在⊙O上,
∴CD是⊙O的切线;
(2)设⊙O的半径为R,则OD=R,OE=R+1,
∵CD是⊙O的切线,
∴∠EDO=90°,
∴ED2+OD2=OE2,
∴32+R2=(R+1)2,
解得R=2,
∴⊙O的半径为2.
看了如图,已知AB为⊙O的直径,A...的网友还看了以下:
读图,回答下列问题(1)A、B两点的经纬度是A、B.(2)图中范围,按东西半球划分,位于西半球的是 2020-04-24 …
如图,质量为M=2.0kg的小车静止在光滑水平面上,小车AB部分是半径为R=0.4m的四分之一圆弧 2020-07-10 …
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向 2020-07-12 …
如图所示,半径R=1.0m的光滑圆弧轨道固定在竖直平面内,轨道的一个端点B和圆心O的连线与水平方向 2020-07-12 …
下列说法正确的是[]A.如果线段AB与线段CD不相交,则线段AB与CD平行.B.两条直线被第三条直 2020-07-23 …
A是有机羧酸盐HCOONa,B、C、D是常见化合物;A、B、C、D焰色应呈黄色,水溶液均呈碱性,其 2020-07-24 …
A是有机羧酸盐HCOONa,B、C、D是常见化合物;A、B、C、D焰色反应呈黄色,水溶液均呈碱性, 2020-07-24 …
对命题“对顶角相等”的说法正确的是A.前提是对顶角,结论“相等”.B.前提是“两个角是对顶角”,结 2020-08-01 …
匀质铁链悬挂在天花板上,其中A点是最低点.C点是悬挂点,B点是介于A、C之间的某一点,关于这三点铁链 2020-11-20 …
成语积累-加点成语的使用错误的一项是()A.共同的爱好和相似的性格使他们有一种一见如故的感觉.B.想 2020-11-23 …