早教吧作业答案频道 -->数学-->
如图1,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE且点A、D、E在同一直线上,连接BE.(1)若∠ACB=60°,则∠AEB的度数为;线段AD、BE之间的数量关系是;(2)若∠ACB=
题目详情
如图1,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE且点A、D、E在同一直线上,连接BE.
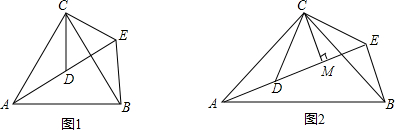
(1)若∠ACB=60°,则∠AEB的度数为___;线段AD、BE之间的数量关系是___;
(2)若∠ACB=n°,用n表示∠AEB并说明理由;
(3)如图2,若∠ACB=∠DCE=90°,点M是DE的中点.若CM=7,BE=10,试求AB的长.(请写全必要的证明和计算过程)

(1)若∠ACB=60°,则∠AEB的度数为___;线段AD、BE之间的数量关系是___;
(2)若∠ACB=n°,用n表示∠AEB并说明理由;
(3)如图2,若∠ACB=∠DCE=90°,点M是DE的中点.若CM=7,BE=10,试求AB的长.(请写全必要的证明和计算过程)
▼优质解答
答案和解析
(1)∵∠ACD+∠DCB=60°,∠DCB+∠BCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CDA=∠CEB,AD=BE,
∵∠CDA=180°-∠CDE=120°,∠CED=60°,
∴∠AEB=120°-60°=60°;
故答案为:60°,相等;
(2)如图1,
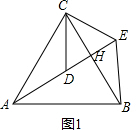 ∵∠ACB=∠DCE,
∵∠ACB=∠DCE,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠AHC=∠BHE,
∴∠AEB=∠ACB=n;
(3)如图2,∵点M是DE的中点,
∴CM=DM,
∵△CDE是等腰直角三角形,
∴CM⊥DE,CM=DM=7,
∴DE=2CM=14,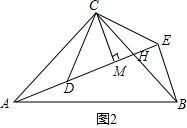
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
,
∴△ACD≌△BCE,
∴AD=BE=10,∠CAD=∠CBE,
∵∠AHC=∠BHE,
∴∠AEB=∠ACH=90°,
∵AE=AD+DE=24,
∴AB=
=
=26.
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴∠CDA=∠CEB,AD=BE,
∵∠CDA=180°-∠CDE=120°,∠CED=60°,
∴∠AEB=120°-60°=60°;
故答案为:60°,相等;
(2)如图1,
 ∵∠ACB=∠DCE,
∵∠ACB=∠DCE,∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∵∠AHC=∠BHE,
∴∠AEB=∠ACB=n;
(3)如图2,∵点M是DE的中点,
∴CM=DM,
∵△CDE是等腰直角三角形,
∴CM⊥DE,CM=DM=7,
∴DE=2CM=14,

∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD与△BCE中,
|
∴△ACD≌△BCE,
∴AD=BE=10,∠CAD=∠CBE,
∵∠AHC=∠BHE,
∴∠AEB=∠ACH=90°,
∵AE=AD+DE=24,
∴AB=
| AE2+BE2 |
| 242+102 |
看了如图1,△ABC和△CDE均为...的网友还看了以下:
如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE.(1)求证:AF=CE;(2 2020-04-09 …
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F 2020-05-14 …
如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN. 2020-05-16 …
四边形ABCD、BEFG均为菱形,如图,四边形ABCD、BGEF均为菱形,A、B、E三点在同一直线 2020-05-16 …
在matlab中如何筛选得出的结果,我只需要多个结果中大于0,小于1的数clc; a0=300;b 2020-05-16 …
如图反比例函数Y=K/X(x> 0 )的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于 2020-06-27 …
(1/2)已知锐角三角形ABC的两条高BD、CE相交于点O,且OB=OC,求证:(1)三角形ABC 2020-06-27 …
如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N,证明:(1)B 2020-08-03 …
如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,分别作▱ABFD与▱ACG 2020-08-03 …
如图,四边形ABCD、BEFG均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥ 2020-11-03 …