早教吧作业答案频道 -->数学-->
如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,分别作▱ABFD与▱ACGE,连接AF,CE.(1)当点D在△ABC外,如图1,求证:AF=CE,AF⊥CE;(2)当点D在△ABC内,如图2,问题(1)中的结论
题目详情
如图,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,分别作▱ABFD与▱ACGE,连接AF,CE.
(1)当点D在△ABC外,如图1,求证:AF=CE,AF⊥CE;
(2)当点D在△ABC内,如图2,问题(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
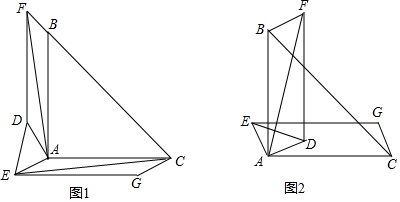
(1)当点D在△ABC外,如图1,求证:AF=CE,AF⊥CE;
(2)当点D在△ABC内,如图2,问题(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.

▼优质解答
答案和解析
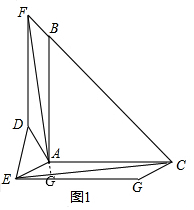 证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∵四边形ABFD是平行四边形,
∴AD=BF,AD∥BF,
∴BF=AE,
∵AD∥BF,
∴∠DAB+∠FBA=180°,
∵∠DAE=∠BAC=90°,
∴∠DAB+∠EAC=180°,
∴∠EAC=∠FBA,
在△EAC和△FBA中,
∵
,
∴△EAC≌△FBA(SAS),
∴EC=AF,∠AFB=∠AEC,
延长FA交EC于G,
∵AD∥FB,
∴∠AFB=∠DAF,
∴∠DAF=∠AEC,
∵∠DAE=90°,
∴∠DAF+∠EAG=90°,
∴∠AEC+∠EAG=90°,
∴∠AGE=90°,
∴AF⊥BC;
(2)如图2,结论仍然成立,理由是: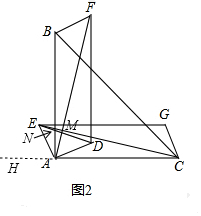
同理得:AB=AC,BF=AE,
作射线CA至H,则∠HAE+∠EAC=180°,
∵BF∥AD,
∴∠FBA+∠BAD=180°,
∵∠BAH=∠EAD=90°,
∴∠HAE+∠EAB=90°,∠BAD+∠EAB=90°,
∴∠HAE=∠BAD,
∴∠EAC=∠FBA,
∴△EAC≌△FBA,
∴AF=EC,∠BAF=∠ECA,
设CE与AB交于N,AF与EC交于点M,
∵∠BAC=90°,
∴∠ECA+∠ANC=90°,
∴∠BAF+∠ANC=90°,
∴∠AME=90°,
∴AF⊥EC.
 证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,
证明:(1)如图1,∵△ABC与△ADE都是等腰直角三角形,∴AB=AC,AD=AE,
∵四边形ABFD是平行四边形,
∴AD=BF,AD∥BF,
∴BF=AE,
∵AD∥BF,
∴∠DAB+∠FBA=180°,
∵∠DAE=∠BAC=90°,
∴∠DAB+∠EAC=180°,
∴∠EAC=∠FBA,
在△EAC和△FBA中,
∵
|
∴△EAC≌△FBA(SAS),
∴EC=AF,∠AFB=∠AEC,
延长FA交EC于G,
∵AD∥FB,
∴∠AFB=∠DAF,
∴∠DAF=∠AEC,
∵∠DAE=90°,
∴∠DAF+∠EAG=90°,
∴∠AEC+∠EAG=90°,
∴∠AGE=90°,
∴AF⊥BC;
(2)如图2,结论仍然成立,理由是:

同理得:AB=AC,BF=AE,
作射线CA至H,则∠HAE+∠EAC=180°,
∵BF∥AD,
∴∠FBA+∠BAD=180°,
∵∠BAH=∠EAD=90°,
∴∠HAE+∠EAB=90°,∠BAD+∠EAB=90°,
∴∠HAE=∠BAD,
∴∠EAC=∠FBA,
∴△EAC≌△FBA,
∴AF=EC,∠BAF=∠ECA,
设CE与AB交于N,AF与EC交于点M,
∵∠BAC=90°,
∴∠ECA+∠ANC=90°,
∴∠BAF+∠ANC=90°,
∴∠AME=90°,
∴AF⊥EC.
看了 如图,△ABC与△ADE都是...的网友还看了以下:
平面向量a,b,e,满足|e|=1,ae=1,be=2,|a-b|=2则ab的最小值|a-b|=2 2020-04-05 …
关于量子力学的用角动量量子化J=n*(hbar)推rn和En的过程中:圆轨道给出mv^2/r=e^ 2020-05-15 …
2^2-1^2=2*1+13^2-2^2=2*2+14^2-3^2=2*3+1……(n+1)^2- 2020-05-19 …
已知三角形的三个顶点分别为A(6,-7),B(-2,3),C(2,1),求AC边上的中线所在的直线 2020-06-03 …
E^2*R/(R+r)^2=E^2/(R-r)^2/R+4r(某公式推导最后两行)本人只得:=E^ 2020-06-07 …
根式计算化简1、(1/x^2-3x+2)+(1/x^2-x)+(1/x^2+x)+(1/x^2+3 2020-07-30 …
(2/3)E是角ACB的外角平分线,同样过A点分别作BD和CE的垂线,垂足为F,G;请问在(1), 2020-08-03 …
5x^2+16x+12=12x^2-29x+15=12x^2-25xy+12y^2=20a^2+42 2020-10-31 …
maple不等方程组solve({-(-u^3/3-e*u^2/2+u)>-(e^2+4)^(3/2 2020-10-31 …
求一道预备班数学期中考试的答案小明在做题时发现了一个规律:1*2/1=1-2/1,2*3/1=2/1 2020-11-05 …