早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.(1)证明:GF=CE.(2)试求五边形ABCFE的面积.
题目详情
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
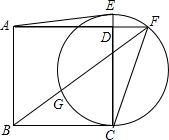
(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.

(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.
▼优质解答
答案和解析
(1)证明:连接AG,GH,
∵正方形ABCD,
∴∠BCD=∠ADC=90°,AB=BC,
∵CE为圆的直径,
∴BC是圆的切线,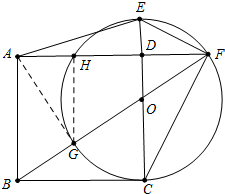
∴BC2=BG•BF,
∴AB2=BG•BF,
∴
=
,
∵∠ABG=∠FBA,
∴△ABG∽△FBA,
∴∠AGB=∠BAF=90°,
∴AG2=AB2-BG2=AD2-DF2=(AD+DF)(AD-DF)=AF(AD-AF),
∵CE为圆的直径,∠ADC=90°,
∴DF=DH,
∴AG2=AF•AH,
∴
=
,
∵∠FAG=∠GAH,
∴△AGH∽△AFG,
∴∠AHG=∠AGF=90°,
∴FG是圆的直径,
∴FG=CE;
(2) 设BG=DF=DH=x,圆的半径为R,则BF=x+2R,AF=2+x,DE=2R-2,由勾股定理和相交弦定理得到,
BO2=CB2+CO2,CD•DE=DF•DH,
∴(x+R)2=R2+22,2(2R-2)=x2,
∴x2+2xR=4,4R-4=x2,
∴4R-4+2xR=4,
∴4R+2xR=8,
∴2R+xR=4,
∴S五边形ABCFE=S正方形ABCD+S△ADE+S△ECF=2+2R+xR=2+4=6.
∵正方形ABCD,
∴∠BCD=∠ADC=90°,AB=BC,
∵CE为圆的直径,
∴BC是圆的切线,

∴BC2=BG•BF,
∴AB2=BG•BF,
∴
| AB |
| BF |
| BG |
| AB |
∵∠ABG=∠FBA,
∴△ABG∽△FBA,
∴∠AGB=∠BAF=90°,
∴AG2=AB2-BG2=AD2-DF2=(AD+DF)(AD-DF)=AF(AD-AF),
∵CE为圆的直径,∠ADC=90°,
∴DF=DH,
∴AG2=AF•AH,
∴
| AG |
| AF |
| AH |
| AG |
∵∠FAG=∠GAH,
∴△AGH∽△AFG,
∴∠AHG=∠AGF=90°,
∴FG是圆的直径,
∴FG=CE;
(2) 设BG=DF=DH=x,圆的半径为R,则BF=x+2R,AF=2+x,DE=2R-2,由勾股定理和相交弦定理得到,
BO2=CB2+CO2,CD•DE=DF•DH,
∴(x+R)2=R2+22,2(2R-2)=x2,
∴x2+2xR=4,4R-4=x2,
∴4R-4+2xR=4,
∴4R+2xR=8,
∴2R+xR=4,
∴S五边形ABCFE=S正方形ABCD+S△ADE+S△ECF=2+2R+xR=2+4=6.
看了 如图,已知正方形ABCD的边...的网友还看了以下:
已知f(x)=lnx(x>0),f(x)的导数是f′(x),若a=f(7),b=f′(12),c= 2020-05-14 …
已知f(x)=x^3+x(x属于R),a,b,c也属于R,且a+b大于0,b+c大于0,c+a大于 2020-05-16 …
设栈S的初始状态为空,元素a,b,c,d,e,f依次入栈S,出栈的序列为b,d,f,e,c,a…… 2020-05-17 …
甲、乙两个身高相同的人抬着一个木箱沿斜坡上山,木箱的悬点恰好在抬杠的中央.如图所示,则甲、乙两人所 2020-06-12 …
已知集合A={正方体},B={长方体},C={正四棱柱},D={直四棱柱},E={棱柱},F={直 2020-06-27 …
已知A是一种常见金属,F是一种红褐色沉淀.试根据图中转化关系,回答下列问题.(1)写出A、C、F、 2020-07-05 …
已知函数f(x)满足f(1+x)=f(1-x),且对任意的x1,x2>1(x1≠x2),有f(x1 2020-07-14 …
如图所示,矩形ABCD的周长为14cm,E为AB的中点,以A为圆心,AE长为半径画弧交AD于点F. 2020-07-14 …
如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4 2020-08-02 …
(2014•海门市模拟)图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第 2020-11-01 …