早教吧作业答案频道 -->数学-->
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.(1)求证:△ABP≌△ACQ.(2)判断△APQ的形状,并说明理由.
题目详情
如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
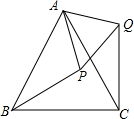
(1)求证:△ABP≌△ACQ.
(2)判断△APQ的形状,并说明理由.

(1)求证:△ABP≌△ACQ.
(2)判断△APQ的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵
,
∴△ABP≌△ACQ(SAS);
(2) △APQ为等边三角形,
理由:∵△ABP≌△ACQ,
∴AP=AQ,∠BAP=∠CAQ,
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
∴AB=AC.
在△ABP与△ACQ中,
∵
|
∴△ABP≌△ACQ(SAS);
(2) △APQ为等边三角形,
理由:∵△ABP≌△ACQ,
∴AP=AQ,∠BAP=∠CAQ,
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
看了如图,等边△ABC中,点P在△...的网友还看了以下:
已知M,P是两个不等的非空集合,则必有() A.空集属于M交P B.空集等于M交P,C.空集包含于 2020-05-16 …
高等数学13-13设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)= 2020-06-02 …
高等数学——概率设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=P 2020-06-02 …
关于概率的:假定用血清蛋白诊断肝癌,设C={被检测者患有肝癌},A={诊断出被检测者患有肝癌},已 2020-06-13 …
简单的概率题请帮解答加分设A,B,C为三个随机事件,且P(A)=P(B)=P(C)=1/4P(AB 2020-07-14 …
求P(ABC)=?不是P(A)P(B)P(C)利用p(ab)=p(a|b)*p(b)这个公式推导出 2020-07-22 …
三角形周长面积问题“三角形三边为a,b,c,则面积S=根号[p*(p-a)*(p-b)*(p-c) 2020-07-31 …
已知a、b、c、d、p都是有理数,根号p是无理数,a不等于0求a+c根号p/a+b根号p=a+d根 2020-08-01 …
请教三角形的几个己和恒等式的证明设I,O分别是三角形ABC的内心与外心,p为半周长,a、b、c为边 2020-08-03 …
7,如果事件ABC相互独立,则下列等式中正确的是()A,P(A+B+C)=P(A)+P(B)+P(C 2020-12-01 …