早教吧作业答案频道 -->数学-->
直线MN与直线PQ相交于O,点A在射线OP上运动,点B在射线OM上运动.(1)如图1,若∠AOB=80°,已知AE、BE分别是∠BAO和∠ABO的角平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?
题目详情
直线MN与直线PQ相交于O,点A在射线OP上运动,点B 在射线OM上运动.
(1)如图1,若∠AOB=80°,已知AE、BE分别是∠BAO和∠ABO的角平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
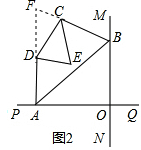
(2)如图2,若∠AOB=80°,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,AD、BC的延长线交于点F,点A、B在运动的过程中,∠F=___;DE、CE又分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小也不发生变化,其大小为:∠CED=___.
(3)如图3,若∠AOB=90°,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF=___;
(4)如图3,若∠AOB=90°,在△AEF中,如果有一个角是另一个角的4倍,则∠ABO的度数=___.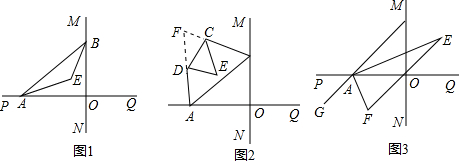
(1)如图1,若∠AOB=80°,已知AE、BE分别是∠BAO和∠ABO的角平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,若∠AOB=80°,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,AD、BC的延长线交于点F,点A、B在运动的过程中,∠F=___;DE、CE又分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小也不发生变化,其大小为:∠CED=___.
(3)如图3,若∠AOB=90°,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F,则∠EAF=___;
(4)如图3,若∠AOB=90°,在△AEF中,如果有一个角是另一个角的4倍,则∠ABO的度数=___.

▼优质解答
答案和解析
 (1)∠AEB的大小不变,
(1)∠AEB的大小不变,
∵直线MN与直线PQ相交于O,
∴∠AOB=80°,
∴∠OAB+∠OBA=80°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=
∠OAB,∠ABE=
∠ABO,
∴∠BAE+∠ABE=
(∠OAB+∠ABO)=40°,
∴∠AEB=140°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ相交于O,
∴∠AOB=80°,
∴∠OAB+∠OBA=80°,
∴∠PAB+∠MBA=280°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=
∠BAP,∠ABC=
∠ABM,
∴∠BAD+∠ABC=
(∠PAB+∠ABM)=140°,
∴∠F=40°,
∴∠FDC+∠FCD=140°,
∴∠CDA+∠DCB=220°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=115°,
∴∠E=65°;
故答案为:50°,65°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=
∠BAO,∠EOQ=
∠BOQ,
∴∠E=∠EOQ-∠EAO=
(∠BOQ-∠BAO)=
∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°;
故答案为:90°;
(4)在△AEF中,∵有一个角是另一个角的4倍,故有:
①∠EAF=4∠E,∠E=22.5°,∠ABO=45°;
②∠EAF=4∠F,∠E=67.5°,∠ABO=135°(舍去);
③∠F=4∠E,∠E=18°,∠ABO=36°;
④∠E=4∠F,∠E=72°,∠ABO=144°(舍去).
∴∠ABO为36°或45°.
故答案为:36°或45°.
 (1)∠AEB的大小不变,
(1)∠AEB的大小不变,∵直线MN与直线PQ相交于O,
∴∠AOB=80°,
∴∠OAB+∠OBA=80°,
∵AE、BE分别是∠BAO和∠ABO角的平分线,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BAE+∠ABE=
| 1 |
| 2 |
∴∠AEB=140°;
(2)∠CED的大小不变.
延长AD、BC交于点F.
∵直线MN与直线PQ相交于O,
∴∠AOB=80°,
∴∠OAB+∠OBA=80°,
∴∠PAB+∠MBA=280°,
∵AD、BC分别是∠BAP和∠ABM的角平分线,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BAD+∠ABC=
| 1 |
| 2 |
∴∠F=40°,
∴∠FDC+∠FCD=140°,
∴∠CDA+∠DCB=220°,
∵DE、CE分别是∠ADC和∠BCD的角平分线,
∴∠CDE+∠DCE=115°,
∴∠E=65°;
故答案为:50°,65°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E=∠EOQ-∠EAO=
| 1 |
| 2 |
| 1 |
| 2 |
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°;
故答案为:90°;
(4)在△AEF中,∵有一个角是另一个角的4倍,故有:
①∠EAF=4∠E,∠E=22.5°,∠ABO=45°;
②∠EAF=4∠F,∠E=67.5°,∠ABO=135°(舍去);
③∠F=4∠E,∠E=18°,∠ABO=36°;
④∠E=4∠F,∠E=72°,∠ABO=144°(舍去).
∴∠ABO为36°或45°.
故答案为:36°或45°.
看了直线MN与直线PQ相交于O,点...的网友还看了以下:
如图直线y=-3/4+8分别交x轴,y轴于A,B两点,线段A,B垂直平分线C,E分别交于x轴y轴于 2020-05-16 …
如图 △ABC中 点O是AC边上的一个动点 过点O作直线MN‖BC 设MN交∠BCA的平分线于E 2020-05-16 …
如图,AD为△ABC的角平分线,E为BC的中点,过E作EF∥AD,交AB于点M,交CA的延长线F, 2020-06-03 …
问当三角形ABC满足什么条件时,四边形AECF是正方形?请说明.三角形ABC中,点O是AC边上的一 2020-06-04 …
如图,AD为△ABC的角平分线,E为BC的中点,过E作EF∥AD,交AB于点M,交CA的延长线F, 2020-06-06 …
在三角形ABC中,点O是AC边上的一个动点,过点O在作直线MN平行BC,设MN交角BCA的平分线于 2020-06-07 …
已知在三角形ABC中,AC=BC,∠CAB=∠CBA=45°,CD是∠ACB的平分线,点E是AB上 2020-07-17 …
如图,已知△ABC≌△DFE,∠B与∠F,∠C与∠E是对应角.有下列结论1.BC=FE2.∠C的平 2020-08-01 …
如图,在三角形ABC中,点O是AC边上一个动点在三角形ABC中,点O是AC边上一动点,过点O做直线 2020-08-03 …
△ABC中,∠ABC=∠ACB,BD平分∠ABC,BD的延长线交△ABC的外角∠ACM的平分线于E, 2021-01-02 …