早教吧作业答案频道 -->数学-->
如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.(1)求证:△ABF≌△CBE;(2)填空:用等式表示线段FA、FE、FC之间的数量关系为.
题目详情
如图,点E为正方形ABCD外一点,点F是线段AE上一点,在△EBF中,∠EBF=90°,BF=BE,连接CE、CF.
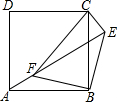
(1)求证:△ABF≌△CBE;
(2)填空:用等式表示线段FA、FE、FC之间的数量关系为___.

(1)求证:△ABF≌△CBE;
(2)填空:用等式表示线段FA、FE、FC之间的数量关系为___.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,
,
∴△ABF≌△CBE(SAS).
(2) 结论:FE2=FA2+FC2.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形,
∵FE2=FC2+EC2,
∵△ABF≌△CBE,
∴AF=EC,
∴FE2=FA2+FC2.
故答案为FE2=FA2+FC2.
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,

∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,
|
∴△ABF≌△CBE(SAS).
(2) 结论:FE2=FA2+FC2.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形,
∵FE2=FC2+EC2,
∵△ABF≌△CBE,
∴AF=EC,
∴FE2=FA2+FC2.
故答案为FE2=FA2+FC2.
看了如图,点E为正方形ABCD外一...的网友还看了以下:
抛物线y=ax的平方+bx+c经过a[-1,0]b[3,0]c[0,3]三点其顶点为d连接bd点p 2020-05-16 …
在空间有n个点分别标记为点1234……n任意两点间均用一电阻为R的导线相连接再把一和点n接到电动势 2020-06-14 …
(2014•长汀县模拟)正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.(1)如图1 2020-06-15 …
如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF 2020-07-17 …
如图,AB是O的直径,C是弧AB的中点,连接AC并延长至D,使DC=CA,连接DB,点E为OB的中 2020-07-21 …
正方形ABCD中,O为对角线AC的中点,P为AC上一点,连接BP,过点P作BP⊥PE,PE交直线C 2020-07-24 …
为什么说过点P曲线的切线可能存在两种情况一为点P就是切点二为点P不是切点 2020-07-31 …
已知正方形ABCD中,边长为4,E为AB边上的一动点,(E为A,B点不重合),设AE=x,以E为顶 2020-08-03 …
为什么直流电接触单边会没事?书本上说人体安全电压是36伏,但为什么即使用万用表一边点直流正极,一边点 2020-12-04 …
农用三轮车电路改装…求高人!本人三轮车有电启动,电瓶是12v的,我想加一个车载充电器给我的看戏机充电 2021-01-15 …