早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点P(x,y)满足约束条件:.(1)在给定的坐标系中画出满足约束条件的可行域(用阴影表示,并注明边界的交点);(2)设,求u的取值范围;(3)已知两
题目详情
在平面直角坐标系中,点P(x,y)满足约束条件: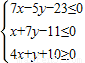 .
.
(1)在给定的坐标系中画出满足约束条件的可行域 (用阴影表示,并注明边界的交点);
(2)设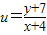 ,求u的取值范围;
,求u的取值范围;
(3)已知两点M(2,1),O(0,0),求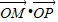 的最大值.
的最大值.
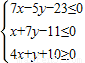 .
.(1)在给定的坐标系中画出满足约束条件的可行域 (用阴影表示,并注明边界的交点);
(2)设
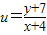 ,求u的取值范围;
,求u的取值范围;(3)已知两点M(2,1),O(0,0),求
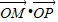 的最大值.
的最大值.
▼优质解答
答案和解析
分析:
(1)先根据直线定出区域的边界,不等式确定区域,由约束条件画出可行域;(2),利用u的几何意义求最值,只需求出何时可行域内的点与点(-4,-7)连线的斜率的最值,从而得到 u的取值范围.(3)先根据向量的数量积公式得出=2x+y,设z=2x+y,再利用z的几何意义求最值,只需求出直线z=2x+y经过点A时,z取到最大值,从而得到答案即可.
(1)由得,∴A(4,1)…(1分)由得,∴B(-1,-6)…(2分)由得,∴C(-3,2)…(3分)画出可行域N,如右下图所示…(4分)(2).…(5分)当直线DP与直线DB重合时,倾斜角最小且为锐角,此时; …(6分)当直线DP与直线DC重合时,倾斜角最大且为锐角,此时kDC=9; …..(7分)所以的取值范围为.…(8分)(3),…..(10分)设z=2x+y,则y=-2x+z,…..…(11分)z表示直线y=-2x+z在y轴上的截距,…(12分)当直线y=-2x+z经过点A时,z取到最大值,…(13分)这时z的最大值为zmax=2×4+1=9.….(14分)
点评:
本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.
分析:
(1)先根据直线定出区域的边界,不等式确定区域,由约束条件画出可行域;(2),利用u的几何意义求最值,只需求出何时可行域内的点与点(-4,-7)连线的斜率的最值,从而得到 u的取值范围.(3)先根据向量的数量积公式得出=2x+y,设z=2x+y,再利用z的几何意义求最值,只需求出直线z=2x+y经过点A时,z取到最大值,从而得到答案即可.
(1)由得,∴A(4,1)…(1分)由得,∴B(-1,-6)…(2分)由得,∴C(-3,2)…(3分)画出可行域N,如右下图所示…(4分)(2).…(5分)当直线DP与直线DB重合时,倾斜角最小且为锐角,此时; …(6分)当直线DP与直线DC重合时,倾斜角最大且为锐角,此时kDC=9; …..(7分)所以的取值范围为.…(8分)(3),…..(10分)设z=2x+y,则y=-2x+z,…..…(11分)z表示直线y=-2x+z在y轴上的截距,…(12分)当直线y=-2x+z经过点A时,z取到最大值,…(13分)这时z的最大值为zmax=2×4+1=9.….(14分)
点评:
本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.
看了在平面直角坐标系中,点P(x,...的网友还看了以下:
先画一个长5厘米,宽2厘米的长方形,并用阴影表示出它的八分之三,算一算,阴影部分的面积是多少平方厘 2020-06-03 …
1、只用{弹簧测力计水瓶子(无刻度)}测1个橡皮泥的密度.并表示橡皮泥的密度的表达式2、只用{量筒 2020-06-15 …
破折号:1、表注释2、表插说3、表提示4、表话题转移5、表话未说完1、我向里面望了一下—阴天,暗得 2020-07-07 …
读下图(阴影部分为黑夜),完成下列要求:1.左图中弧线BAC为晨昏线的一段,请将其转绘到右图中,并用 2020-11-01 …
在边长4米的正方形草地上两对角各有一棵树树上各拴着一只羊栓羊的绳子各长四米.请把两只羊同时吃到的地用 2020-11-01 …
在平面直角坐标系中,点P(x,y)满足约束条件:.(1)在给定的坐标系中画出满足约束条件的可行域(用 2020-11-03 …
“绿树浓阴夏日长,楼台倒影入池塘”是晚唐诗人高骈在《山亭夏日》中的诗句,描写了酷夏特有的情趣,并表达 2020-11-04 …
请在下面直线上任意取一点O,并以O点为圆心画一个直径为4厘米的圆.在圆上挖取一个最大的正方形.(剩下 2020-11-26 …
读来自南北半球光照示意图,完成以下各题.(1)在图中画出晨昏线,用阴影表示夜半球,并标出晨线.(2) 2020-11-27 …
读下图,完成下列问题。(1)画出北半球夏至日太阳照射地球示意图,并用阴影表示黑夜。(2)画出黄赤交角 2021-01-23 …