早教吧作业答案频道 -->数学-->
如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.(1)设OB=OC=1,BD=y,CE=x,求y关于x的函数关系式;(不
题目详情
如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.
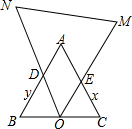
(1)设OB=OC=1,BD=y,CE=x,求y关于x的函数关系式;(不要求写x的取值范围)
(2)在上题中,连结DE,设DE=m,△ODE的面积为s,求s关于m的函数关系式.(不要求写m的取值范围).

(1)设OB=OC=1,BD=y,CE=x,求y关于x的函数关系式;(不要求写x的取值范围)
(2)在上题中,连结DE,设DE=m,△ODE的面积为s,求s关于m的函数关系式.(不要求写m的取值范围).
▼优质解答
答案和解析
(1)∵△ABC、△OMN均为等边三角形,
∴∠B=∠C=60°,∠DOE=60°,
∴∠BDO+∠BOD=∠BOD+∠EOC=120°,
∴∠BDO=∠EOC,
∴△BOD∽△COE
∴
=
,
即
=
,
∴y=
;
(2)∵△BOD∽△COE,
∴
=
,
∵BO=CO,
∴
=
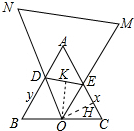
,
∵∠DOE=∠C=60°,
∴△DOE∽△OCE,
∴∠DEO=∠OEC,
作OH⊥EC于H,OK⊥DE于K,
∴OH=OK=
,
∴s=
•m•
=
m.
∴∠B=∠C=60°,∠DOE=60°,
∴∠BDO+∠BOD=∠BOD+∠EOC=120°,
∴∠BDO=∠EOC,
∴△BOD∽△COE
∴
| BD |
| OC |
| BO |
| CE |
即
| y |
| 1 |
| 1 |
| x |
∴y=
| 1 |
| x |
(2)∵△BOD∽△COE,
∴
| DO |
| OE |
| BO |
| EC |
∵BO=CO,
∴
| DO |
| CO |
| OE |
| EC |

∵∠DOE=∠C=60°,
∴△DOE∽△OCE,
∴∠DEO=∠OEC,
作OH⊥EC于H,OK⊥DE于K,
∴OH=OK=
| ||
| 2 |
∴s=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
看了如图,△ABC、△OMN均为等...的网友还看了以下:
设直线l的方程是2x+By-1=0,倾斜角为α.(1)试将α表示为B的函数;(2)若π6<α<2π 2020-04-11 …
最搞不清这类概念题了OJL.设集合A=R,集合B=R+,则从集合A到集合B的函数f只可能是A.f: 2020-05-24 …
直角三角形两个锐角∠A与∠B的函数关系是()A.正比例函数B.一次函数C.反比例函数D.二次函数 2020-07-26 …
设f(x)是连续函数,x=a与x=b是方程f(x)=0的两个相邻实根证明若已知在(a,b)内一点c 2020-08-01 …
关于函数定义的问题~书上说“设A,B都是非空的数的集合,f是从A到B的一个对应法则,那么映射f:A 2020-08-02 …
函数题,A是不是B的函数(1)A等边三角形的面积B等边三角形的边长这两者是不是函数关系,A是不是B 2020-08-03 …
设A到B的函数为f1:x→y=2x+1B到C的函数f2:y→z=y2-1则A到C的函数f是A.f:z 2020-10-30 …
提问5天无一人能解.望能人踊跃进入过边长为a的正三角形ABC的中心O作任意直线交AB、AC于E、F两 2020-12-25 …
设单调函数y=p(x)的定义域为D,值域为A,如果单调函数y=q(x)使得函数y=p(q(x))的置 2020-12-31 …
设对应法则f是从集合A到集合B的函数,则下列结论中正确的是.(1)B必是由A中数对应的输出值组成的集 2020-12-31 …