已知函数y=-12x(x>0)3x(x<0)的图象如图所示，点P是y轴负半轴上一动点，过点P作y轴的垂线交图象于A，B两点，连接OA、OB．下列结论：①若点M1（x1，y1），M2（x2，y2）在图象上，且x1<x2<0

Question

已知函数y=

-(12)/(x)(x>0)

(3)/(x)(x<0)

的图象如图所示，点P是y轴负半轴上一动点，过点P作y轴的垂线交图象于A，B两点，连接OA、OB．下列结论：
①若点M₁（x₁，y₁），M₂（x₂，y₂）在图象上，且x₁<x₂<0，则y₁<y₂；
②当点P坐标为（0，-3）时，△AOB是等腰三角形；
③无论点P在什么位置，始终有S_△AOB=7.5，AP=4BP；
④当点P移动到使∠AOB=90°时，点A的坐标为（2√(6)，-√(6)）．
其中正确的结论个数为（　　）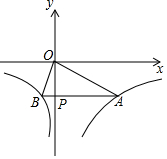

A. 1

B. 2

C. 3

D. 4

Answer 1

①错误．∵x₁2<0，函数y随x是增大而减小，
∴y₁>y₂，故①错误．
②正确．∵P（0，-3），
∴B（-1，-3），A（4，-3），
∴AB=5，OA=√(32+42)=5，
∴AB=AO，
∴△AOB是等腰三角形，故②正确．
③正确．设P（0，m），则B（(3)/(m)，m），A（-(12)/(m)，m），
∴PB=-(3)/(m)，PA=-(12)/(m)，
∴PA=4PB，
∵S_AOB=S_△OPB+S_△OPA=(3)/(2)+(12)/(2)=7.5，故③正确．
④正确．设P（0，m），则B（(3)/(m)，m），A（-(12)/(m)，m），
∴PB=-(3)/(m)，PA=-(12)/(m)，OP=-m，
∵∠AOB=90°，∠OPB=∠OPA=90°，
∴∠BOP+∠AOP=90°，∠AOP+∠OPA=90°，
∴∠BOP=∠OAP，
∴△OPB∽△APO，
∴(OP)/(AP)=(PB)/(OP)，
∴OP²=PB•PA，
∴m²=-(3)/(m)•（-(12)/(m)），
∴m⁴=36，
∵m<0，
∴m=-√(6)，
∴A（2√(6)，-√(6)），故④正确．
∴②③④正确，
故选C．