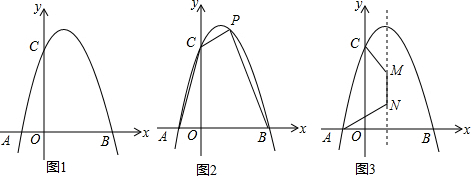
如图1，抛物线y=ax2+bx+c（a≠0）与x轴交于点A、B，与y轴交于点C，且A（-1，0），OB=OC=3OA．（1）试求抛物线的解析式；（2）如图2，点P是第一象限抛物线上的一点，连接AC、PB、PC．且S四边形OBPC

Question

如图1，抛物线y=ax²+bx+c（a≠0）与x轴交于点A、B，与y轴交于点C，且A（-1，0），OB=OC=3OA．
（1）试求抛物线的解析式；
（2）如图2，点P是第一象限抛物线上的一点，连接AC、PB、PC．且S_{四边形OBPC}=5S_△AOC，试求点P的坐标？
（3）如图3，定长为1的线段MN在抛物线的对称轴上上下滑动，连接CM、AN．记m=CM+MN+AN，试问：m是否有最小值？如果有，请求m的最小值；如果没有，请说明理由．

Answer 1

{"title":"

\uff081\uff09\u7531A\uff08-1\uff0c0\uff09\uff0cOB=OC=3OA\uff0c\u5f97
OB=OC=3\uff0c
\u5373B\uff083\uff0c0\uff09\uff0cC\uff080\uff0c3\uff09\uff0c
\u628aA\uff0cB\uff0cC\u7684\u5750\u6807\u4ee3\u5165\u51fd\u6570\u89e3\u6790\u5f0f\uff0c\u5f97

\u89e3\u5f97

\u629b\u7269\u7ebf\u7684\u89e3\u6790\u5f0f\u4e3ay=-x^{2+2x+3\uff1b
\uff082\uff09\u4f5cPM\u22a5x\u8f74\u4ea4BC\u4e8eM\u70b9\uff0c\u5982\u56fe1
\uff0c
\u7531B\uff083\uff0c0\uff09\uff0cC\uff080\uff0c3\uff09\uff0c\u5f97BC\u7684\u89e3\u6790\u5f0f\u4e3ay=-x+3\uff0c
\u8bbeP\u70b9\u5750\u6807\u4e3a\uff08n\uff0c-n2+2n+3\uff09\uff0cM\uff08n\uff0c-n+3\uff09\uff0e
PM\u7684\u957f\u4e3a-n2+2n+3-\uff08-n+3\uff09=-n2+3n\uff0c
S_{\u25b3AOC=AO\u2022OC=}}

S_{\u56db\u8fb9\u5f62OBPC=S\u25b3OBC+S\u25b3PBC}

             _{=\u00d73\u00d73+\u00d73\uff08-n^2+3n\uff09}

            =-n²⁺

\u7531S_{\u56db\u8fb9\u5f62OBPC=5S\u25b3AOC\uff0c}

\u5f97-n^{2+n+=\u00d75\uff0e}

\u5316\u7b80\uff0c\u5f97

n^{2-3n+2=0\uff0c
\u89e3\u5f97n_{1=1\uff0cn2=2\uff0c
P\u70b9\u5750\u6807\u4e3a\uff081\uff0c4\uff09\uff082\uff0c3\uff09\uff1b
\uff083\uff09m\u6709\u6700\u5c0f\u503c\uff0c\u7406\u7531\u5982\u4e0b\uff1a
\u5728OC\u4e0a\u4f5cCC\u2032=MN=1\uff0c\u5982\u56fe2
\uff0c
\u4f5cC\u2032\u5173\u4e8e\u5bf9\u79f0\u8f74\u7684\u5bf9\u79f0\u70b9\uff0c\u8fde\u63a5C\u2033A\uff0c
CM+AN=AC\u2033\u53d6\u5f97\u6700\u5c0f\u503c\u4e3aC\u2033A\uff0e
\u5728Rt\u25b3ADC\u2033\u4e2d\uff0c\u7531\u52fe\u80a1\u5b9a\u7406\uff0c\u5f97}}

m\u6700\u5c0f=CM+MN+AN=C\u2033A+MN=1+

" "latex":"

\uff081\uff09\u7531A\uff08-1\uff0c0\uff09\uff0cOB=OC=3OA\uff0c\u5f97
OB=OC=3\uff0c
\u5373B\uff083\uff0c0\uff09\uff0cC\uff080\uff0c3\uff09\uff0c
\u628aA\uff0cB\uff0cC\u7684\u5750\u6807\u4ee3\u5165\u51fd\u6570\u89e3\u6790\u5f0f\uff0c\u5f97
$\\left \\{ {{\\begin{array}{ll} {a-b+c=0} \\\\ {9a+3b+c=0} \\\\ {c=3} \\end{array}}} \\right .$

\u89e3\u5f97$\\left \\{ {{\\begin{array}{ll} {a=-1} \\\\ {b=2} \\\\ {c=3} \\end{array}}} \\right .$

\u629b\u7269\u7ebf\u7684\u89e3\u6790\u5f0f\u4e3ay=-x^{2+2x+3\uff1b
\uff082\uff09\u4f5cPM\u22a5x\u8f74\u4ea4BC\u4e8eM\u70b9\uff0c\u5982\u56fe1
\uff0c
\u7531B\uff083\uff0c0\uff09\uff0cC\uff080\uff0c3\uff09\uff0c\u5f97BC\u7684\u89e3\u6790\u5f0f\u4e3ay=-x+3\uff0c
\u8bbeP\u70b9\u5750\u6807\u4e3a\uff08n\uff0c-n2+2n+3\uff09\uff0cM\uff08n\uff0c-n+3\uff09\uff0e
PM\u7684\u957f\u4e3a-n2+2n+3-\uff08-n+3\uff09=-n2+3n\uff0c
S_{\u25b3AOC=$\\dfrac {1} {2}$AO\u2022OC=$\\dfrac {1} {2}\\times 1\\times 3=\\dfrac {3} {2}$}}

S_{\u56db\u8fb9\u5f62OBPC=S\u25b3OBC+S\u25b3PBC}

             _{=$\\dfrac {1} {2}$\u00d73\u00d73+$\\dfrac {1} {2}$\u00d73\uff08-n^2+3n\uff09}

            =-$\\dfrac {3} {2}$n^{2+$\\dfrac {9} {2}n+\\dfrac {9} {2}$}

\u7531S_{\u56db\u8fb9\u5f62OBPC=5S\u25b3AOC\uff0c}

\u5f97-$\\dfrac {3} {2}$n^{2+$\\dfrac {9} {2}$n+$\\dfrac {9} {2}$=$\\dfrac {3} {2}$\u00d75\uff0e}

\u5316\u7b80\uff0c\u5f97

n^{2-3n+2=0\uff0c
\u89e3\u5f97n_{1=1\uff0cn2=2\uff0c
P\u70b9\u5750\u6807\u4e3a\uff081\uff0c4\uff09\uff082\uff0c3\uff09\uff1b
\uff083\uff09m\u6709\u6700\u5c0f\u503c\uff0c\u7406\u7531\u5982\u4e0b\uff1a
\u5728OC\u4e0a\u4f5cCC\u2032=MN=1\uff0c\u5982\u56fe2
\uff0c
\u4f5cC\u2032\u5173\u4e8e\u5bf9\u79f0\u8f74\u7684\u5bf9\u79f0\u70b9\uff0c\u8fde\u63a5C\u2033A\uff0c
CM+AN=AC\u2033\u53d6\u5f97\u6700\u5c0f\u503c\u4e3aC\u2033A\uff0e
\u5728Rt\u25b3ADC\u2033\u4e2d\uff0c\u7531\u52fe\u80a1\u5b9a\u7406\uff0c\u5f97}}

$C''A=\\sqrt {{AD}^{2}+{C''D}^{2}}=\\sqrt {{(2+1)}^{2}+{2}^{2}}=\\sqrt {13}$

m\u6700\u5c0f=CM+MN+AN=C\u2033A+MN=1+$\\sqrt {13}$

"}

作业帮用户 2017-09-19 举报