早教吧作业答案频道 -->数学-->
问题提出平面上,若点P与A、B、C三点中的任意两点均构成等腰三角形,则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形,也称点P是△ABC的巧妙点.初步思考(1)如图①,在等边△
题目详情
问题提出
平面上,若点P与A、B、C三点中的任意两点均构成等腰三角形,则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形,也称点P是△ABC的巧妙点.
初步思考
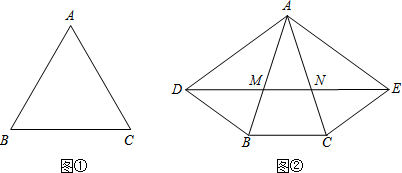
(1)如图①,在等边△ABC的内部和外部各作一个△ABC的巧妙点.(尺规作图,不写作法,保留作图痕迹)
(2)如图②,在△ABC中,AB=AC,∠BAC=36°,点D、E是△ABC的两个巧妙点,其中AD=AB,AE=AC,BD=BC=CE,连接DE,分别交AB、AC于点M、N.求证:DA2=DB•DE.
深入研究
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P可能为△ABC的巧妙点吗?若可能,请画出示意图,并直接写出∠BAC的度数;若不可能,请说明理由.
平面上,若点P与A、B、C三点中的任意两点均构成等腰三角形,则称点P是A、B、C三点的巧妙点.若A、B、C三点构成三角形,也称点P是△ABC的巧妙点.
初步思考
(1)如图①,在等边△ABC的内部和外部各作一个△ABC的巧妙点.(尺规作图,不写作法,保留作图痕迹)
(2)如图②,在△ABC中,AB=AC,∠BAC=36°,点D、E是△ABC的两个巧妙点,其中AD=AB,AE=AC,BD=BC=CE,连接DE,分别交AB、AC于点M、N.求证:DA2=DB•DE.
深入研究
(3)在△ABC中,AB=AC,若存在一点P,使PB=BA,PA=PC.点P可能为△ABC的巧妙点吗?若可能,请画出示意图,并直接写出∠BAC的度数;若不可能,请说明理由.

▼优质解答
答案和解析
(1)如图①;
(2)∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
在△ADB和△ABC中
∴△ADB≌△ABC,
同理:△ACE≌△ABC.
∴∠BAD=∠BAC=∠CAE=36°,∠ADB=∠ABD=∠ABC=72°,
∴∠DAE=∠BAD+∠BAC+∠CAE=108°,
∵AD=AB=AC=AE,
∴∠ADE=∠AED=36°=∠BAD,
∴∠BDM=∠BDA-∠MDA=36°,
∠BMD=∠ADM+∠DAM=72°=∠ABD,
∴DB=DM.
∵∠DBM=∠ABD,∠AED=∠BAD,
∴△DAM∽△DEA,
∴
=
,
∴DA2=DM•DE,
∵DM=DB,
∴DA2=DB•DE.
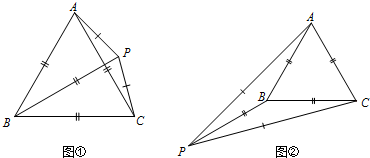
(3)
第一种如图①或图②(只需画一个即可),∠BAC=60°.
第二种如图③,∠BAC=36°;
第三种如图④,∠BAC=108°;
第四种如图⑤,∠BAC=120°.
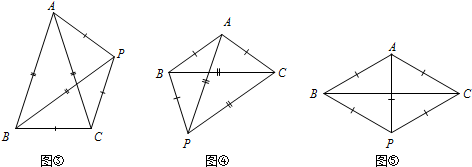
以上共四种:60°、36°、108°、120°.


(2)∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°,
在△ADB和△ABC中
|
∴△ADB≌△ABC,
同理:△ACE≌△ABC.
∴∠BAD=∠BAC=∠CAE=36°,∠ADB=∠ABD=∠ABC=72°,
∴∠DAE=∠BAD+∠BAC+∠CAE=108°,
∵AD=AB=AC=AE,
∴∠ADE=∠AED=36°=∠BAD,
∴∠BDM=∠BDA-∠MDA=36°,
∠BMD=∠ADM+∠DAM=72°=∠ABD,
∴DB=DM.
∵∠DBM=∠ABD,∠AED=∠BAD,
∴△DAM∽△DEA,
∴
| DM |
| DA |
| DA |
| DE |
∴DA2=DM•DE,
∵DM=DB,
∴DA2=DB•DE.
(3)
第一种如图①或图②(只需画一个即可),∠BAC=60°.

第二种如图③,∠BAC=36°;
第三种如图④,∠BAC=108°;
第四种如图⑤,∠BAC=120°.

以上共四种:60°、36°、108°、120°.
看了问题提出平面上,若点P与A、B...的网友还看了以下:
如图,在四边形ABCD中,过点BD的中点任作一条直线L,分别交AO、BC于E、F(1)OE与OF相 2020-06-04 …
一副扑克牌有52张,以惯例A为1点,依此类推,J为11点,Q为12点,K为13点.任意抽出若干牌, 2020-06-12 …
以知两点坐标,如何知道在两点连线上任意点的坐标在直角坐标系中,已经知道两点的坐标,在次两点的连线上 2020-06-14 …
对于平面上任意n个点构成的点集P,如果其中任意两点之间距离均已确定,那么就成这个点集是“稳定的”. 2020-07-30 …
我们把平面内与四边形各边端点构成的三角形都是等腰三角形的点叫做这个四边形的腰点,例如:如图,矩形A 2020-07-30 …
cad里面怎样在任意斜线上任意拾取点(例如距离端点20mm处)作为另一直线的起点.cad里面怎样在 2020-07-30 …
如何用三角形的三个坐标表示三角形中的任意一点坐标,如:三角形ABC,A(x1,y1)B(x2,y2) 2020-10-31 …
阅读材料,并按要求回答问题。2016年5月9日,国务院办公厅印发促进科技成果转移转化行动方案的通知。 2020-11-21 …
“如果他不能完成这项任务,那你就更不能完成了”这句话是什么意思?“如果他不能完成这项任务,那你就更不 2020-11-27 …
(本小题满分13分)如图,已知抛物线,过点任作一直线与相交于两点,过点作轴的平行线与直线相交于点(为 2020-12-05 …