早教吧作业答案频道 -->数学-->
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为()A.30°B.45°C.60°D.90°
题目详情
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是AB、AD的中点,则异面直线B1C与EF所成的角的大小为( )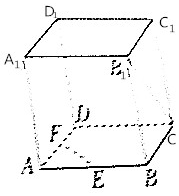
A. 30°
B. 45°
C. 60°
D. 90°
▼优质解答
答案和解析
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,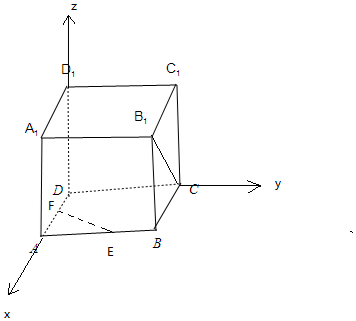
设正方体ABCD-A1B1C1D1中棱长为2,
则E(2,1,0),F(1,0,0),B1(2,2,2),C(0,2,0),
=(-2,0,-2),
=(-1,-1,0),
设异面直线B1C与EF所成的角为θ,
则cosθ=
=
=
,
∴θ=60°.
故选:C.

设正方体ABCD-A1B1C1D1中棱长为2,
则E(2,1,0),F(1,0,0),B1(2,2,2),C(0,2,0),
| B1C |
| EF |
设异面直线B1C与EF所成的角为θ,
则cosθ=
|
| ||||
|
|
| 2 | ||||
|
| 1 |
| 2 |
∴θ=60°.
故选:C.
看了如图所示,在正方体ABCD-A...的网友还看了以下:
设f(z),g(z)都在简单闭曲线c上及c内解析,且在c上f(z)=g(z),证明:在c内也有f( 2020-05-15 …
数学分析题》》关于连续的设f:D->实数,|f|:D->实数因为|f|(x)=|f(x)|举一个例 2020-06-03 …
设f(z),g(z)都在简单闭曲线c上及c内解析,且在c上f(z)=g(z),证明:在c内也有f( 2020-06-18 …
如图所示表示两个相干波源S1、S2产生的波在同一种均匀介质中相遇.图中实线表示波峰,虚线表示波谷, 2020-07-04 …
设函数f(x)在x=0处连续,且limh→0f(h2)h2=1,则()A.f(0)=0且f−′(0 2020-07-20 …
f(x)在[a,b]连续,在(a,b)二阶连续可导,证明存在c,使f(a)+f(b)-2f((a+ 2020-07-25 …
高数!求详解设f(x)在[0,1]上连续,在(0,1)内二阶可导,且f(0)=f(1)=0,证明: 2020-07-29 …
关于积分中值定理的题设f(x)在[a,b]上连续,在(a,b)内可导,且存在c∈(a,b),使得∫ 2020-07-31 …
关于泰勒公示展开求证:已知f(x)在[a,b]存在二阶导数,f'(a)=f'(b)=0,则在存在c∈ 2020-11-23 …
已知函数f(x)=ax+b/x+c(a>0)的图像在点,(1,f(1))处的切线方程为y=x-1.( 2020-12-08 …