早教吧作业答案频道 -->数学-->
已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为12,右焦点为F2,点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两
题目详情
已知椭圆C:
+
=1(a>b>0)的离心率为
,右焦点为F2,点M在圆x2+y2=b2上,且M在第一象限,过M作圆x2+y2=b2的切线交椭圆于P,Q两点.若△PF2Q的周长为4,则椭圆C的方程为___.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
▼优质解答
答案和解析
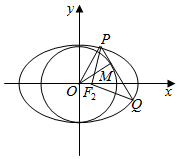 椭圆C:
椭圆C:
+
=1(a>b>0)的离心率为
,则a=2c,b=
c,
设P(x1,y1),Q(x2,y2),
∴|PF2|2=(x1-c)2+y12=
(x1-4c)2,
∴|PF2|=2c-
x1,
连接OM,OP,由相切条件知:
|PM|2=|OP|2-|OM|2=x12+y12-3c2=
x12,
∴|PM|=
x1,
∴|PF2|+|PM|=2c,
同理可求|QF2|+|QM|=2c,
∴|F2P|+|F2Q|+|PQ|=4c.
∵△PF2Q的周长为4,∴c=1,
∴a=2,b=
,
∴椭圆C的方程为
+
=1.
故答案为
+
=1.
 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
设P(x1,y1),Q(x2,y2),
∴|PF2|2=(x1-c)2+y12=
| 1 |
| 4 |
∴|PF2|=2c-
| 1 |
| 2 |
连接OM,OP,由相切条件知:
|PM|2=|OP|2-|OM|2=x12+y12-3c2=
| 1 |
| 4 |
∴|PM|=
| 1 |
| 2 |
∴|PF2|+|PM|=2c,
同理可求|QF2|+|QM|=2c,
∴|F2P|+|F2Q|+|PQ|=4c.
∵△PF2Q的周长为4,∴c=1,
∴a=2,b=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
故答案为
| x2 |
| 4 |
| y2 |
| 3 |
看了已知椭圆C:x2a2+y2b2...的网友还看了以下:
不用太详细,简要回答就行,(1)过点(0,1)且与曲线y=x+1/x-1在点(3不用太详细,简要回 2020-04-13 …
1.已知一次函数y=kx+b(k≠0)的图象经过点(0,1),且y随x的增大而增大,请你写出一个符 2020-05-16 …
已知抛物线的顶点经过点(2,1),且经过点(-1,4),求此二次函数的关系式 2020-05-19 …
直线被两平行线截得线段的题目怎么样做?1.过点(2,0),且平行于y轴的直线l被两平行直线2x-y 2020-05-21 …
若x2+xy+y2=1且x、y∈R,则n=x2+y2的取值范围是()A.0<n≤1B.2≤n≤3C 2020-05-22 …
已知椭圆过点(0,1)且离心率为二分之根三求椭圆的方程,2,a一a二为椭左右顶点直线x等于二倍根二 2020-06-21 …
微分方程y''=x的经过点(0,1)且在此点与直线y=1/2x+1相切的积分曲线是A.1/6x^3 2020-07-09 …
已知f(x)=ax^4+bx^2+c的图象过点(0.1),且再x=1处的切线方程时y=x-2.求y 2020-08-01 …
求下列条件的圆的标准方程,要带方法和简便方法哦~1以P1[4,9和P26,3为直径的两端点2圆心为 2020-08-02 …
设与直线x-y-1=0与直线x-y-1=0经过点(2,-1)且圆心在直线2x+y=0上求这个圆的方程 2021-01-11 …