早教吧作业答案频道 -->数学-->
如图,已知抛物线y2=4x,过点P(2,0)作斜率分别为k1,k2的两条直线,与抛物线相交于点A、B和C、D,且M、N分别是AB、CD的中点(1)若k1+k2=0,AP=2PB,求线段MN的长;(2)若k1•k2=-1,求△PMN
题目详情
如图,已知抛物线y2=4x,过点P(2,0)作斜率分别为k1,k2的两条直线,与抛物线相交于点A、B和C、D,且M、N分别是AB、CD的中点
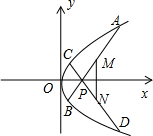
(1)若k1+k2=0,
=2
,求线段MN的长;
(2)若k1•k2=-1,求△PMN面积的最小值.

(1)若k1+k2=0,
| AP |
| PB |
(2)若k1•k2=-1,求△PMN面积的最小值.
▼优质解答
答案和解析
(1)设A(x1,y1),B(x2,y2),不妨设y1>0,则
设直线AB的方程为y=k1(x-2),代入y2=4x,可得y2-
y-8=0
∴y1+y2=
,y1y2=-8,
∵
=2
,∴y1=-2y2,∴y1=4,y2=-2,
∴yM=1,
∵k1+k2=0,
∴线段AB和CD关于x轴对称,
∴线段MN的长为2;
(2)∵k1•k2=-1,∴两直线互相垂直,
设AB:x=my+2,则CD:x=-
y+2,
x=my+2代入y2=4x,得y2-4my-8=0,
则y1+y2=4m,y1y2=-8,
∴M(2m2+2,2m).
同理N(
+2,-
),
∴|PM|=2|m|•
,|PN|=
•
,|
∴S△PMN=
|PM||PN|=
(m2+1)=2(|m|+
)≥4,
当且仅当m=±1时取等号,
∴△PMN面积的最小值为4.
设直线AB的方程为y=k1(x-2),代入y2=4x,可得y2-
| 4 |
| k1 |
∴y1+y2=
| 4 |
| k1 |
∵
| AP |
| PB |
∴yM=1,
∵k1+k2=0,
∴线段AB和CD关于x轴对称,
∴线段MN的长为2;
(2)∵k1•k2=-1,∴两直线互相垂直,
设AB:x=my+2,则CD:x=-
| 1 |
| m |
x=my+2代入y2=4x,得y2-4my-8=0,
则y1+y2=4m,y1y2=-8,
∴M(2m2+2,2m).
同理N(
| 2 |
| m2 |
| 2 |
| m |
∴|PM|=2|m|•
| m2+1 |
| 2 |
| m2 |
| m2+1 |
∴S△PMN=
| 1 |
| 2 |
| 1 |
| |m| |
| 1 |
| |m| |
当且仅当m=±1时取等号,
∴△PMN面积的最小值为4.
看了如图,已知抛物线y2=4x,过...的网友还看了以下:
已知函数f(x)=kx3-3(k+1)x2-k2+1(k>0),若f(x)的单调递减区间是(0,4 2020-05-23 …
关于x的方程(k2-1x2)+(k+1)x+2=0急~(1)当k取何值时,此方程为一元二次方程?并 2020-06-07 …
(2011•白云区一模)已知关于x的二次函数y=x2+(2k-1)x+k2-1.(1)若关于x的一 2020-06-11 …
下列各组角中,终边相同的角是()A.k2π与kπ+π2(k∈Z)B.kπ±π3与k3π(k∈Z)C 2020-07-26 …
怎样将k消去y=k2/k2+1x=3/k2+1换成关于xy的方程y=3k/k2+1x=3/k2+1 2020-10-31 …
等腰三角形两腰所在直线的直线方程分别为x+y-2=0,与x-7y-4=0,原点在等腰三角形的底边上, 2020-10-31 …
已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d=|kx0-y0 2020-11-03 …
(2014•大兴区二模)已知:关于x的一元二次方程(k2-1)x2-(3k-1)x+2=0.(1)当 2020-11-12 …
把自然数1,2,…,k2排成一个方阵表:123…kk+1k+2k+3…2k……………(k-1)k+1 2020-11-17 …
求数学高手解决请问这个→(k-k1)/(1-k1*k)=(k2-k)/(1+k*2k)怎么来的,或者 2021-01-14 …