早教吧作业答案频道 -->数学-->
如图,过抛物线y2=2px(p>0)上一点P(1,2),作两条直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时:(1)求y1+y2的值;(2)若直线AB在y轴上的截距b∈[-
题目详情
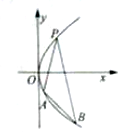
如图,过抛物线y2=2px(p>0)上一点P(1,2),作两条直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时:
(1)求y1+y2的值;
(2)若直线AB在y轴上的截距b∈[-1,3]时,求△ABP面积S△ABP的最大值.

(1)求y1+y2的值;
(2)若直线AB在y轴上的截距b∈[-1,3]时,求△ABP面积S△ABP的最大值.
▼优质解答
答案和解析
(1)∵点P(1,2)在抛物线上,∴22=2p,解得p=2.
设直线PA的斜率为kPA,直线PB的斜率为kPB.
则kPA=
(x1≠1),kPB=
(x2≠1),
∵PA与PB的斜率存在且倾斜角互补,
∴kPA=-kPB.
由A(x1,y1),B(x2,y2)均在抛物线上,得
y12=4x1,①y22=4x2,②
∴y1+2=-(y2+2),∴y1+y2=-4.
(2)由①-②得直线AB的斜率为kAB=-1.
因此设直线AB的方程为y=-x+b,由直线与抛物线方程联立,消去y得x2-(2b+4)x+b2=0,
由△≥0,得b≥-1,这时x1+x2=2b+4,x1x2=b2,
|AB|=4
,又点P到直线AB的距离为d=
,
所以S△ABP=
,
令f(x)=(x+1)(3-x)2(x∈[-1,3]),则由f′(x)=(3x-1)(x-3)=0,得x=
或x=3,
当x∈(-1,
)时,f′(x)>0,所以f(x)单调递增,当x∈(
,3)时,f′(x)>0,所以f(x)单调递减,
故f(x)的最大值为
,故△ABP面积S△ABP的最大值为
.
设直线PA的斜率为kPA,直线PB的斜率为kPB.
则kPA=
| y1-2 |
| x1-1 |
| y2-2 |
| x2-1 |
∵PA与PB的斜率存在且倾斜角互补,
∴kPA=-kPB.
由A(x1,y1),B(x2,y2)均在抛物线上,得
y12=4x1,①y22=4x2,②
∴y1+2=-(y2+2),∴y1+y2=-4.
(2)由①-②得直线AB的斜率为kAB=-1.
因此设直线AB的方程为y=-x+b,由直线与抛物线方程联立,消去y得x2-(2b+4)x+b2=0,
由△≥0,得b≥-1,这时x1+x2=2b+4,x1x2=b2,
|AB|=4
| 2 |
| b+1 |
| |3-b| | ||
|
所以S△ABP=
| 2(b+1)(3-b)2 |
令f(x)=(x+1)(3-x)2(x∈[-1,3]),则由f′(x)=(3x-1)(x-3)=0,得x=
| 1 |
| 3 |
当x∈(-1,
| 1 |
| 3 |
| 1 |
| 3 |
故f(x)的最大值为
| 256 |
| 27 |
16
| ||
| 9 |
看了如图,过抛物线y2=2px(p...的网友还看了以下:
已知方程x^2-7x+8=0的两根为x1,x2,求作一个新的一元二次方程,使它的两根分别为(x1) 2020-05-15 …
已知方程2x的平方减4x减5等于0的根是x1和x2,求下列式子的值.1、x1的平方加x2的平方加x 2020-05-16 …
设X1,X2.X7为正整数,且X1<X2.<X7,X1+X1+X3+.X7=159,求x7-x1的 2020-05-17 …
某质点从静止开始以加速度a1=3m/s2作匀加速直线运动,经5s物体的速度为v1、位移为x1,之后 2020-05-23 …
有一个数据库X1,要求创建一个与X1库结构完全相同且不带任何记录的数据库X2,假定X1已打开,最便捷 2020-05-31 …
已知方程2x的平方+3x-1=0的两根为x1,x2,不解方程,求下列各式的值(1)x1的平方+x2 2020-06-06 …
证明函数单调性题目原题:判断并证明f(x)=x/x2=1在(0,无穷大)上的单调性设x1,x2再用 2020-08-01 …
有理数x1,x2表示数轴上得到点A1,A2,我们就把x1,x2叫做A1,A2的一维坐标.一般地称| 2020-08-03 …
已知x1,x2,...,x2012都是不等于0的有理数(1)若y1=x1分之x1的绝对值,则y1=( 2020-10-31 …
已知一元二次方程x2-x-3=0的较小根为x1,则下面对x1的估计正确的是()A.-2<x1<-1B 2020-11-12 …