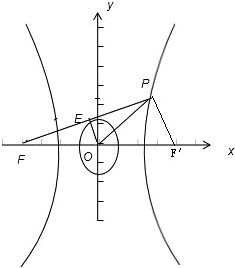
过双曲线x2a2-y2b2=1(a>0，b>0)的左焦点F（-c，0）（c>0）作圆x2+y2=a24的切线，切点为E，延长FE交双曲线右支于点P．若OP=2OE-OF，则双曲线的渐近线方程为（）A.10x±2y=0B.2x±10y=0C.6x±2y=0

Question

过双曲线

(x2)/(a2)-(y2)/(b2)=1(a>0，b>0)的左焦点F（-c，0）（c>0）作圆x2+y2=(a2)/(4)的切线，切点为E，延长FE交双曲线右支于点P．若

OP

=2

OE

-

OF

，则双曲线的渐近线方程为（　　）

A.

√(10)x±2y=0

B. 2x±

√(10)y=0

C.

√(6)x±2y=0

D. 2x±

√(6)y=0

Answer 1

∵

OP

=2

OE

-

OF

，
∴

OE

=(1)/(2)（

OP

+

OF

）
∴E为PF的中点，令右焦点为F′，则O为FF′的中点，
则PF′=2OE=a，
∵E为切点，
∴OE⊥PF
∴PF′⊥PF
∵PF-PF′=2a
∴PF=PF′+2a=3a
在Rt△PFF′中，PF²+PF′²=FF′²
即9a²+a²=4c²=4（a²+b²），
∴3a²=2b²，
∴(b)/(a)=(√(6))/(2)，
∴渐近线方程为y=±(√(6))/(2)x，即√(6)x±2y=0，
故选：C