早教吧作业答案频道 -->数学-->
在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF,(点E、F为折痕与矩形ABCD边的交点),再将纸片还原.(1)若点P落在矩形ABCD的边AB上(如图①).①当点P与点A重
题目详情
在矩形ABCD中,AB=8,AD=6,现将纸片折叠,点D的对应点记为点P,折痕为EF,(点E、F为折痕与矩形ABCD边的交点),再将纸片还原.
(1)若点P落在矩形ABCD的边AB上(如图①).
①当点P与点A重合时,∠DEF___;当点E与点A重合时,∠DEF=___;
②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时菱形DEPF的边长.
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值.
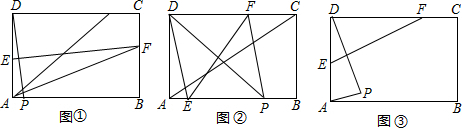
(1)若点P落在矩形ABCD的边AB上(如图①).
①当点P与点A重合时,∠DEF___;当点E与点A重合时,∠DEF=___;
②当点E在AB上,点F在DC上时(如图②),求证:四边形DEPF为菱形,并直接写出当AP=7时菱形DEPF的边长.
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值.

▼优质解答
答案和解析
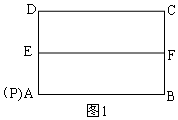 (1)①当点P与点A重合时,如图1,
(1)①当点P与点A重合时,如图1,
∴EF是AD的中垂线,
∴∠DEF=90°,
当点E与点A重合时,如图2,
此时∠DEF=
∠DAB=45°,
故答案为:90°,45°;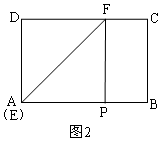
②当点E在AB上,点F在DC上时,如图3,
∵EF是PD的中垂线,
∴DO=PO,EF⊥PD,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EPO,
∵∠DOF=∠EOP,
∴△DOF≌△POE(ASA),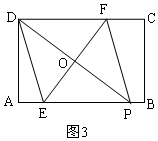
∴DF=PE,
∵DF∥PE,
∴四边形DEPF是平行四边形,
∵EF⊥PD,
∴▱DEPF为菱形,
当AP=7时,设菱形的边长为x,则AE=7-x,DE=x,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴62+(7-x)2=x2,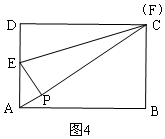
x=
,
∴当AP=7时,设菱形的边长为
;
(2)若点P落在矩形ABCD的内部,且点E、F分别在AD、DC边上,
如图4,当F与C重合,点P在对角线AC上时,AP有最小值,
由折叠得:CD=PC=8,
由勾股定理得:AC=
=10,
∴AP=10-8=2,
则AP的最小值是2.
 (1)①当点P与点A重合时,如图1,
(1)①当点P与点A重合时,如图1,∴EF是AD的中垂线,
∴∠DEF=90°,
当点E与点A重合时,如图2,
此时∠DEF=
| 1 |
| 2 |
故答案为:90°,45°;

②当点E在AB上,点F在DC上时,如图3,
∵EF是PD的中垂线,
∴DO=PO,EF⊥PD,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠FDO=∠EPO,
∵∠DOF=∠EOP,
∴△DOF≌△POE(ASA),

∴DF=PE,
∵DF∥PE,
∴四边形DEPF是平行四边形,
∵EF⊥PD,
∴▱DEPF为菱形,
当AP=7时,设菱形的边长为x,则AE=7-x,DE=x,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴62+(7-x)2=x2,

x=
| 85 |
| 14 |
∴当AP=7时,设菱形的边长为
| 85 |
| 14 |
(2)若点P落在矩形ABCD的内部,且点E、F分别在AD、DC边上,
如图4,当F与C重合,点P在对角线AC上时,AP有最小值,
由折叠得:CD=PC=8,
由勾股定理得:AC=
| 62+82 |
∴AP=10-8=2,
则AP的最小值是2.
看了在矩形ABCD中,AB=8,A...的网友还看了以下:
把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做,根据是. 2020-05-14 …
f(x)=x^11+ax^9+cx^5-8(a,c为常数)若f(-2)=10求f(2) 2020-05-20 …
现有纸片:4张边长为a的正方形,3张边长为b的正方形,8张宽为a、长为b的长方形,用这15张纸片重 2020-06-03 …
现有纸片:4张边长为a的正方形,3张边长为b的正方形,8张宽为a、长为b的长方形,用这15张纸片重 2020-06-03 …
若一个三角形的三边长分别为1、a、8(其中a为正整数),则以a-2、a、a+2为边的三角形的面积为 2020-06-06 …
同步卫星星下点轨迹8字形,为什莫?我觉得是0形呀!急!快高考了,求答案呀!解释一下8字形各特殊点对 2020-06-10 …
如果a/b=8(a,b为非零自然数),那么a和B最大公因数是(),最小公倍数是()再加一题如果a和 2020-07-13 …
七巧板能否拼成凸的7和8边形.为什么?若能帮拼下不能说出为什么不是正的七八多边形我要证明过程详细一 2020-07-14 …
(1)已知A+B=3x-5x+1,A-C=-2x+3x-5,求当x=2时B+C的值;提示:B+C=( 2020-10-31 …
A的伴随矩阵A*=diag(1,1,1,8)求|A||A*|=8=|A|^3,为什么?A*=|A|乘 2021-02-10 …