如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=2;正确的是()A.4个B.3个C.2个D.1个
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=
;正确的是( )2 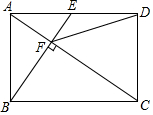
A. 4个
B. 3个
C. 2个
D. 1个
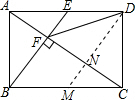 如图,过D作DM∥BE交AC于N,
如图,过D作DM∥BE交AC于N,∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴
| AE |
| BC |
| AF |
| CF |
∵AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AF |
| CF |
| 1 |
| 2 |
∴CF=2AF,故②正确;
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=
| 1 |
| 2 |
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正确;
设AE=a,AB=b,则AD=2a,
由△BAE∽△ADC,有
| b |
| a |
| 2a |
| b |
| 2 |
∴tan∠CAD=
| CD |
| AD |
| b |
| 2a |
| ||
| 2 |
故选B.
设函数f(x)在[a,b]上连续,在(a,b)内可导,且f'(x)不等于0.试证明存在x1,x2属 2020-05-14 …
e^a*e^b等于e^ab吗?e^a-e^b=e^b*(e^(a/b)-1)对吗?那e^a/e^b 2020-06-10 …
A,B,C,D,E5个人参加一个国际会议,其中,1,B和C他们讲西班牙语,但是和D在一起的时候他们 2020-06-12 …
设A,B均为n阶方阵,E为n阶单位阵,且(A-E)(B-E)=0A=E或B=E|A-E|=0或|B 2020-06-18 …
A,B均为三阶可逆矩阵,且A^3=0,则A:E-A,E+A均不可逆?B:E-A不可逆但E+A可逆? 2020-07-20 …
设矩阵A=ααT,其中α是n维列向量,又已知αTα=1.(1)证明A2=A;(2)证明B=E+A+ 2020-07-20 …
设函数f(x)在闭区间[a,b]上连续,在(a,b)内可导,且f^'(x)≠0.试证存在ξ,η∈( 2020-07-21 …
有关区间的定义问题让我们回忆实数集合R中区间的精确定义:R的子集E称为一个区间,如果它至少包含两个点 2020-11-20 …
我在教学生三角形全等的判定时,为了让学生按公理顺序列出三个条件,并能区别几个判定,书写格式要求在△A 2020-11-21 …
e^3b-e^3a/e^b-e^a化为e^2a+e^2b+e^a*e^b的运算过程如题 2021-01-15 …