早教吧作业答案频道 -->数学-->
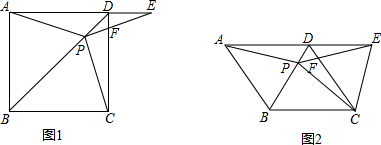
如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当
题目详情
如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F,
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.

▼优质解答
答案和解析
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2) 由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°
(3) AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2) 由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,
即∠CPF=∠EDF=90°
(3) AP=CE;理由如下:
在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
|
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°-∠PFC-∠PCF=180°-∠DFE-∠AEP,
即∠CPF=∠EDF=180°-∠ADC=180°-120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
看了 如图1,在正方形ABCD中,...的网友还看了以下:
三角形ABC的三边是a,b,c满足a平方加b平方加c平方等于ab加ac加cb,试判断三角形ABC的 2020-05-15 …
已知:如图,在Rt三角形ABC中,∠C=90°沿过B点的一条直线BE折叠这个三角形,使C点与AB边 2020-05-22 …
在△ABC中,AB=5,BC=3,AC=4,PQ//AB,P点在AC上(与点A、C重合),Q点在B 2020-07-24 …
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两 2020-07-30 …
如图,在三角形ABC中,点O是AC的一个动点,(O点与A,C不重合),过点O作直线MN平行BC,设 2020-08-03 …
(2014•西宁)如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别 2020-08-03 …
1道初二几何题,Rt三角形ABC中,∠C=90度,M为AC中点,N为CB中点,E为AB中点,证明以C 2020-11-01 …
PS问题求解答()21.用画笔工具做一串珍珠形式的圆点,下面说法正确的是?A.需要勾选去形状动态.散 2020-12-09 …
一张三角形纸,不用任何工具,比较,证明AB与AC长短三角形三点,下面2点是B,C上面1点是A三角形三 2020-12-14 …
等腰直角三角形ABC,C为直角顶点,在AB、AC上分别取点M、N,沿MN对折使顶点C落在斜边AB上, 2020-12-23 …