早教吧作业答案频道 -->数学-->
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.(1)求证:△PHC≌△CFP;(2)证明四边形PEDH和四边形PFBG都是矩形,并直
题目详情
如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H.
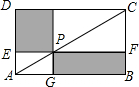
(1)求证:△PHC≌△CFP;
(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.

(1)求证:△PHC≌△CFP;
(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD为矩形,
∴AB∥CD,AD∥BC.
∵PF∥AB,
∴PF∥CD,
∴∠CPF=∠PCH.
∵PH∥AD,
∴PH∥BC,
∴∠PCF=∠CPH.
在△PHC和△CFP中,
,
∴△PHC≌△CFP(ASA).
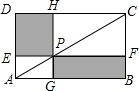
(2)∵四边形ABCD为矩形,
∴∠D=∠B=90°.
又∵EF∥AB∥CD,GH∥AD∥BC,
∴四边形PEDH和四边形PFBG都是矩形.
∵EF∥AB,
∴∠CPF=∠CAB.
在Rt△AGP中,∠AGP=90°,
PG=AG•tan∠CAB.
在Rt△CFP中,∠CFP=90°,
CF=PF•tan∠CPF.
S矩形DEPH=DE•EP=CF•EP=PF•EP•tan∠CPF;
S矩形PGBF=PG•PF=AG•PF•tan∠CAB=EP•PF•tan∠CAB.
∵tan∠CPF=tan∠CAB,
∴S矩形DEPH=S矩形PGBF.
∴AB∥CD,AD∥BC.
∵PF∥AB,
∴PF∥CD,
∴∠CPF=∠PCH.
∵PH∥AD,
∴PH∥BC,
∴∠PCF=∠CPH.
在△PHC和△CFP中,
|
∴△PHC≌△CFP(ASA).

(2)∵四边形ABCD为矩形,
∴∠D=∠B=90°.
又∵EF∥AB∥CD,GH∥AD∥BC,
∴四边形PEDH和四边形PFBG都是矩形.
∵EF∥AB,
∴∠CPF=∠CAB.
在Rt△AGP中,∠AGP=90°,
PG=AG•tan∠CAB.
在Rt△CFP中,∠CFP=90°,
CF=PF•tan∠CPF.
S矩形DEPH=DE•EP=CF•EP=PF•EP•tan∠CPF;
S矩形PGBF=PG•PF=AG•PF•tan∠CAB=EP•PF•tan∠CAB.
∵tan∠CPF=tan∠CAB,
∴S矩形DEPH=S矩形PGBF.
看了 如图,点P在矩形ABCD的对...的网友还看了以下:
如图,四边形ABCD是平行四边形,在ab的延长线上截取be=ab,点f在ae的延长线上,ce和df 2020-05-15 …
如图①,四边形ABCD是平行四边形,对角线AC,BD相交于点O,过点O做直线EF分别交AD,BC于 2020-05-15 …
1.如图,已知菱形ABCD的周长为8cm,∠ABC=120°,求对角线BD和AC及菱形的面积?2. 2020-05-16 …
如图,四边形ABCD是平行四边形,AE⊥CB,交CB的延长线于点E,AF⊥CD,交CD的延长线于点 2020-05-16 …
已知:如图,四边形ABCD是菱形,∠A=60°,直线EF经过点C,分别交AB、AD的延长线于E、F 2020-05-16 …
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于已 2020-05-16 …
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点 2020-05-16 …
如图,四边形ABCD为轴对称图形,对称轴为直线MN,MN与AD相交于点M与BC交于点N,已知三角形 2020-07-17 …
已知:如图,四边形ABCD是菱形,G是AB上任一点,DG交AC于点E.求证:∠AGD=∠CBE,已 2020-08-01 …
如图,四边形ABCD各边相等,且∠ABC为60°,直线L过D点,但与四边形ABCD不相交(D点除外) 2020-11-24 …