早教吧作业答案频道 -->数学-->
在平面直角坐标系中,点A(-4,0),B(0,3),将线段AB向右平移m(m为正数)个单位向下平移1个单位长度到CD,点A、B的对应点分别为C、D.(1)直接写出点C(,),D(,)(用
题目详情
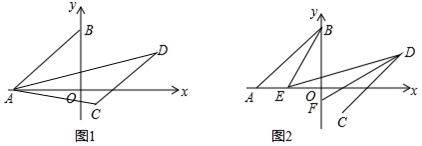
在平面直角坐标系中,点A(-4,0),B(0,3),将线段AB向右平移m(m为正数)个单位向下平移1个单位长度到CD,点A、B的对应点分别为C、D.
(1)直接写出点C(___,___),D(___,___)(用含m的式子表示);
(2)连接AC、AD,若三角形ACD面积是三角形ABO面积的2倍,求m的值;
(3)如图2,在线段OA上取一点E(不与O、A重合),F为y轴负半轴上一点,且FD平分∠CDE,若∠ABE=∠DEO,∠BED=α,求∠ABE+2∠BFD的度数(结果用含α的式子表示).
(1)直接写出点C(___,___),D(___,___)(用含m的式子表示);
(2)连接AC、AD,若三角形ACD面积是三角形ABO面积的2倍,求m的值;
(3)如图2,在线段OA上取一点E(不与O、A重合),F为y轴负半轴上一点,且FD平分∠CDE,若∠ABE=∠DEO,∠BED=α,求∠ABE+2∠BFD的度数(结果用含α的式子表示).

▼优质解答
答案和解析
(1)∵点A(-4,0),B(0,3),将线段AB向右平移m(m为正数)个单位向下平移1个单位长度到CD,
∴C(-4+m,-1),D(m,2),
故答案为-4+m,-1,m,2.
(2)如图1中,过点C作MN∥x轴,作AM⊥MN,DN⊥MN.
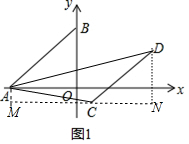
由题意:
(1+3)•(m+4)-
•m•1-
•4•3=2•
•3•4,
解得m=20.
(3)如图2中,作EH∥AB,连接DO延长到G,.设∠ABE=∠DEO=y,∠FDE=∠FDC=x,∠BFD=z.
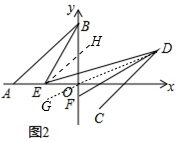
∵AB∥CD,
∴AB∥EH∥CD,
∴∠ABE=∠BEH,∠HED=∠EDC,
∴∠BED=∠ABE+∠EDC,
∴α=y+2x ①
∵∠EOG=∠DEO+∠EDO,∠GOF=∠BFD+∠ODF,
∴∠EOF=∠DEO+∠EDF+∠BFD,
∴x+y+z=90° ②
由①②可得y+2z=180°-α,
∴∠ABE+2∠BFD=180°-α.
∴C(-4+m,-1),D(m,2),
故答案为-4+m,-1,m,2.
(2)如图1中,过点C作MN∥x轴,作AM⊥MN,DN⊥MN.

由题意:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得m=20.
(3)如图2中,作EH∥AB,连接DO延长到G,.设∠ABE=∠DEO=y,∠FDE=∠FDC=x,∠BFD=z.

∵AB∥CD,
∴AB∥EH∥CD,
∴∠ABE=∠BEH,∠HED=∠EDC,
∴∠BED=∠ABE+∠EDC,
∴α=y+2x ①
∵∠EOG=∠DEO+∠EDO,∠GOF=∠BFD+∠ODF,
∴∠EOF=∠DEO+∠EDF+∠BFD,
∴x+y+z=90° ②
由①②可得y+2z=180°-α,
∴∠ABE+2∠BFD=180°-α.
看了 在平面直角坐标系中,点A(-...的网友还看了以下:
关于映射的题设集合A到B的映射为f1:x→y=2x+1,集合B到C的映射为f2:y→z=y²-1,则 2020-03-31 …
设f(x)=(a^x+a^-x)/2g(x)=(a^x-a^-x)/2(其中a>0且a≠1),设f 2020-04-26 …
四个问题是判断对错一个数的因数的个数是无限的()在0.2x5=1中0.2和5是1的因数()一个数的 2020-05-13 …
已知函数f(x)=ax2+(b-8)x-a-ab(a≠0),当x∈(-3,2)时,f(x)>0;当 2020-05-21 …
已知命题p:方程a^2x^2+ax-2=0在[-1,1]上有解.......已知命题p:方程a^2 2020-07-13 …
牛顿冷却模型,实验验证θ=θ0+(θ1-θ0)e—kt(e—kt代表e的负kt次方,θ0与θ1中的 2020-07-16 …
已知f(x)=q,当x=pq(p,q∈N+,pq为既约真分数,0<p<q)0,x为(0,1)中的无 2020-07-26 …
若关于x的不等式x2+ax-2>0在区间[1,5]上有解,则实数a的取值范围为多少?若不等式x2+ 2020-07-31 …
高一恒成立,有解问题(1)方程x²-4x+3b=0在[1,4]有解,b取值范围?(2)不等式x²- 2020-07-31 …
z-x^2y^3=0在(1,1,1)的切平面方程是2求f(x,y)=x^3+y^3-3xy+1的极小 2020-11-01 …