早教吧作业答案频道 -->数学-->
已知△ABC与△ADE是等边三角形,点B、A、D在一条直线上,∠CPN=60°交直线AE与点N;(1)若点P在线段AB上运动,如图1、(不与A、B重合)猜想线段PC、PN的数量关系并证明.(2)若点P在线段AD
题目详情
已知△ABC与△ADE是等边三角形,点B、A、D在一条直线上,∠CPN=60°交直线AE与点N;
(1)若点P在线段AB上运动,如图1、(不与A、B重合)猜想线段PC、PN 的数量关系并证明.
(2)若点P在线段AD上运动、(不与A、D重合),在图2中画出图形,猜想线段PC、PN 的数量关系并证明
(3)总结:若点P在直线AB上运动、(不与A、B、D重合),线段PC、PN 的数量关系会保持不变吗?(不需要写出证明过程)
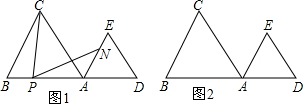
(1)若点P在线段AB上运动,如图1、(不与A、B重合)猜想线段PC、PN 的数量关系并证明.
(2)若点P在线段AD上运动、(不与A、D重合),在图2中画出图形,猜想线段PC、PN 的数量关系并证明
(3)总结:若点P在直线AB上运动、(不与A、B、D重合),线段PC、PN 的数量关系会保持不变吗?(不需要写出证明过程)

▼优质解答
答案和解析
(1)PC=PN;理由如下: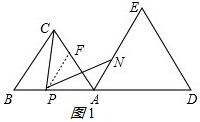
如图1所示,在AC上截取AF=AP,
∵AP=AF,∠BAC=60°,
∴△APF为等边三角形,
∴PF=PA,
∵∠CPF+∠FPN=60°,∠FPN+∠NPA=60°,
∴∠CPF=∠APN,在△PCF和△PNA中,
,
∴△PCF≌△PNA(ASA),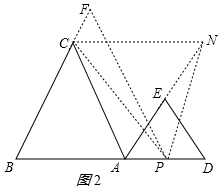
∴PC=PN;
(2)PC=PN;理由如下:
当P在AD上时,∠CPN的一边PN交AE的延长线于N,此时也有PC=PN;
过P作AC的平行线交BC的延长线于F,如图2所示:
∴∠F=∠BCA=60°,∠APF=∠BAC=60°,
∴∠F=∠APF,
∴CF=AP,
∵∠CPN=60°,
∴∠NPF=60°-∠FPC,
∵∠BPC=60°-∠CPF,
∴∠NPF=∠BPC,
∵∠F=∠PAN=60°,
∴∠FCP=∠APN=60°+∠APC,
在△PCF和△NPA中,
,
∴△PCF≌△NPA(AAS),
∴PC=PN;
(3)线段PC、PN的数量关系保持不变;
无论点P在AB上哪个点,都有△PCF≌△PNA,
∴PC,PN的数量关系不变.

如图1所示,在AC上截取AF=AP,
∵AP=AF,∠BAC=60°,
∴△APF为等边三角形,
∴PF=PA,
∵∠CPF+∠FPN=60°,∠FPN+∠NPA=60°,
∴∠CPF=∠APN,在△PCF和△PNA中,
|
∴△PCF≌△PNA(ASA),

∴PC=PN;
(2)PC=PN;理由如下:
当P在AD上时,∠CPN的一边PN交AE的延长线于N,此时也有PC=PN;
过P作AC的平行线交BC的延长线于F,如图2所示:
∴∠F=∠BCA=60°,∠APF=∠BAC=60°,
∴∠F=∠APF,
∴CF=AP,
∵∠CPN=60°,
∴∠NPF=60°-∠FPC,
∵∠BPC=60°-∠CPF,
∴∠NPF=∠BPC,
∵∠F=∠PAN=60°,
∴∠FCP=∠APN=60°+∠APC,
在△PCF和△NPA中,
|
∴△PCF≌△NPA(AAS),
∴PC=PN;
(3)线段PC、PN的数量关系保持不变;
无论点P在AB上哪个点,都有△PCF≌△PNA,
∴PC,PN的数量关系不变.
看了 已知△ABC与△ADE是等边...的网友还看了以下:
175页第24题线段AB等于4,点O是线段AB上一点,点C、D是线段OA、OB的中点,小明很轻松的 2020-05-23 …
请问搴帷览物华这五个字连起来是什么意思!急………在现线等! 2020-06-19 …
作文题目是《我家的一个星期天》根据“表达我家的快乐,充实,和睦的气氛”列一个提纲快块块快在、线等 2020-07-05 …
已知线段a,b(a〉b)作一条线段使它等于2(a-b)1.用直尺作射线AB,2.用圆规在射线AB上 2020-07-14 …
如图,线段AB是一条格点线段.(1)画一条线段,使它与线段AB有一个公共端点.且与线段AB相等.并 2020-07-25 …
给出下列几个命题:①若某平面的两条斜线段相等则它们在此平面上的射影相等;②若两条斜线段在平面上的射 2020-07-30 …
下列结论中正确的个数为()①若过平面外一点引两条斜线段与平面所成的角相等,则斜线段也相等②若平面的 2020-07-30 …
平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等 2020-08-01 …
在平行投影下不平行也不垂直于投射面的线段的投影仍是线段但与原线段不等长这句话哪里对了相当于平行线和 2020-08-02 …
对于平面几何中的命题“夹在两平行线之间的垂线段相等”,在立体几何中,类比上述命题,可以得到命题夹在 2020-08-02 …