早教吧作业答案频道 -->数学-->
四边形ABCD中,E是BC的中点,BC=4,且∠AED=∠B=∠C=60°.(1)如图1,若AD∥BC,求证:△ADE是等边三角形;(2)如图2,若AD不平行于BC,过点E作EM⊥AD于M,求EM的长.
题目详情
四边形ABCD中,E是BC的中点,BC=4,且∠AED=∠B=∠C=60°.
(1)如图1,若AD∥BC,求证:△ADE是等边三角形;
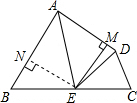
(2)如图2,若AD不平行于BC,过点E作EM⊥AD于M,求EM的长.
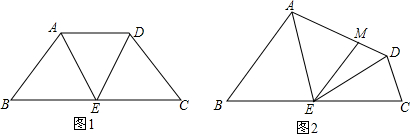
(1)如图1,若AD∥BC,求证:△ADE是等边三角形;
(2)如图2,若AD不平行于BC,过点E作EM⊥AD于M,求EM的长.

▼优质解答
答案和解析
 (1)证明:∵AD∥BC,∠B=∠C=60°,
(1)证明:∵AD∥BC,∠B=∠C=60°,
∴AB=CD,
∵E是BC的中点,
∴BE=CE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE,
∴AE=DE,
又∵∠AED=60°,
∴△ADE是等边三角形;
(2) 过点E作EN⊥AB于点N,
∵∠AED=60°,
∴∠AEB+∠DEC=120°,
∵∠B=60°,
∴∠BAE+∠AEB=120°,
∴∠BAE=∠DEC,
又∵∠B=∠C=60°,
∴△ABE∽△ECD,
∴
=
,
∴AB•ED=EC•EA,
∵E是BC的中点,
∴EB=EC,
∴AB•DE=BE•AE,
∴
=
,
又∵∠AED=∠B=60°,
∴△ABE∽AED,
∴∠BAE=∠DAE,
∵NE⊥AB,EM⊥AD,
∴NE=EM,
∴sin60°=
,
∵BE=EC,
∴
=
=
,
∵BC=4,
∴EM=
.
 (1)证明:∵AD∥BC,∠B=∠C=60°,
(1)证明:∵AD∥BC,∠B=∠C=60°,∴AB=CD,
∵E是BC的中点,
∴BE=CE,
在△ABE和△DCE中,
|
∴△ABE≌△DCE,
∴AE=DE,
又∵∠AED=60°,
∴△ADE是等边三角形;
(2) 过点E作EN⊥AB于点N,
∵∠AED=60°,
∴∠AEB+∠DEC=120°,
∵∠B=60°,
∴∠BAE+∠AEB=120°,
∴∠BAE=∠DEC,
又∵∠B=∠C=60°,
∴△ABE∽△ECD,
∴
| AB |
| EC |
| AE |
| DE |
∴AB•ED=EC•EA,
∵E是BC的中点,
∴EB=EC,
∴AB•DE=BE•AE,
∴
| AB |
| BE |
| AE |
| DE |
又∵∠AED=∠B=60°,
∴△ABE∽AED,
∴∠BAE=∠DAE,
∵NE⊥AB,EM⊥AD,
∴NE=EM,
∴sin60°=
| NE |
| BE |
| ||
| 2 |
∵BE=EC,
∴
| EN |
| BC |
| EM |
| BC |
| ||
| 4 |
∵BC=4,
∴EM=
| 3 |
看了 四边形ABCD中,E是BC的...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
(b-a)(a-c)(c-b)=-[(-b+a)(-a+c)(-c+b)]对吧 也就是在(b-a) 2020-05-16 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
下列能判定△ABC≌△A′B′C′的是()A.AB=A′B′,BC=B′C′,∠C=∠C′B.∠B 2020-07-14 …
高二数学题,帮忙解决,要步骤的(1)设a,b,c属于R,a+b+c=0,abc0.(2)设a,b, 2020-07-22 …
用C(A)表示非空集合A中的元素个数,定义A*B=C(A)-C(B),当C(A)≥C(B)C(B) 2020-08-01 …
3角形3边abc求证:abc≥(a+b-c)(a+c-b)(b+c-a)假设x=a+b-c>0y=a 2020-11-01 …
已知正数abc,且a/b+c=b/c+a=c/a+b=k.则在下列四个点中,在正比例函数y=kx图像 2020-11-01 …
aW、bX、cC、dZ、eR是五种短周期元素,e-d=d-c=c-b=b-a=4,其中一种是常见金属 2020-11-26 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …