早教吧作业答案频道 -->数学-->
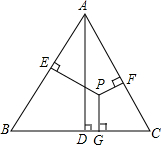
如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.
题目详情
如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G,求证:AD=PE+PF+PG.

▼优质解答
答案和解析
连接PA、PB、PC,如图所示: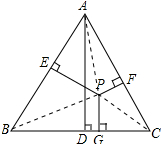
∵S△ABP+S△BCP+S△ACP=S△ABC,
∴
AB•PE+
BC•PD+
AC•PF=
BC•AD,
∵△ABC是等边三角形,
∴AB=BC=AC,
∴
BC(PE+PF+PG)=
BC•AD,
∴PE+PD+PF=AD.

∵S△ABP+S△BCP+S△ACP=S△ABC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等边三角形,
∴AB=BC=AC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴PE+PD+PF=AD.
看了 如图,点P是等边三角形ABC...的网友还看了以下:
1.已知:P={0,1},M={x/x包含于P},则P与M的关系为A.P∈M B.P不属于M C. 2020-05-13 …
求助一个关于C语言指针的问题int main(){x09int a[]={1,2,3,4,5};x 2020-05-13 …
已知抛物线Y等于aX²—2X+c与它的对称轴相较于点A(1,-4),与y轴交与点C,与X轴正半轴交 2020-05-16 …
已知抛物线y=ax^2-2x+c与它的对称轴相交与点A(1,-4),与y轴交于点C,与x轴正半轴交 2020-05-16 …
已知集合M={x|x=3n,n属于Z},N={x|x=3n+1,n属于Z},P={x|x=3n+1 2020-05-16 …
概率论,对于任意A,B,下面结论正确的是对于任意A,B,下面结论正确的是()A.若P(AB)=0, 2020-07-30 …
一道关于数学真假命题的题π为圆周率,a.b.c.d·属于Q,已知命题p:若aπ+b=cπ+d;(1 2020-08-01 …
让自来水流过如图所示装置,当水流稳定后()双选A.P点流速等于Q点流速B.P点流速小于Q点流速C.P 2020-12-20 …
c++关于指针(8)已知数组A和指针p定义为:intA[20][10],*p;,要使p指向A的首元素 2020-12-31 …
已知抛物线Y=ax2-2x+c与它的对称轴相较于点A(1,-4),与Y轴相交于C,与Y轴正半轴交于B 2021-01-10 …