如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（）A.x-y2=3B.2x-y2=9C.3x-y2=15D.4x-y2=21

Question

如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（　　）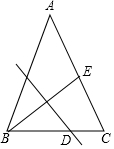

A. x-y²=3

B. 2x-y²=9

C. 3x-y²=15

D. 4x-y²=21

Answer 1

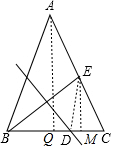
过A作AQ⊥BC于Q，过E作EM⊥BC于M，连接DE，
∵BE的垂直平分线交BC于D，BD=x，
∴BD=DE=x，
∵AB=AC，BC=12，tan∠ACB=y，
∴(EM)/(MC)=(AQ)/(CQ)=y，BQ=CQ=6，
∴AQ=6y，
∵AQ⊥BC，EM⊥BC，
∴AQ∥EM，
∵E为AC中点，
∴CM=QM=(1)/(2)CQ=3，
∴EM=3y，
∴DM=12-3-x=9-x，
在Rt△EDM中，由勾股定理得：x²=（3y）²+（9-x）²，
即2x-y²=9，
故选B．