早教吧作业答案频道 -->数学-->
我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1
题目详情
我们知道对于x轴上的任意两点A(x1,0),B(x2,0),有AB=|x1-x2|,而对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|称为Pl,P2两点间的直角距离,记作d(P1,P2),即d(P1,P2)=|x1-x2|+|y1-y2|.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)=___;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.
(1)已知O为坐标原点,若点P坐标为(1,3),则d(O,P)=___;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=2,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)试求点M(2,3)到直线y=x+2的最小直角距离.
▼优质解答
答案和解析
 (1)d(O,P)=|0-1|+|0-3|=4;
(1)d(O,P)=|0-1|+|0-3|=4;
故答案为:4;
(2)∵O为坐标原点,动点P(x,y)满足d(O,P),
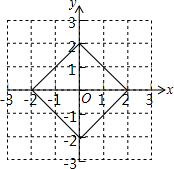
∴|0-x|+|0-y|=|x|+|y|=2,
所有符合条件的点P组成的图形如图所示;
(3)∵d=|x-2|+|y-3|=|x-2|+|x+2-3|
=|x-2|+|x-1|
∴x可取一切实数,|x-2|+|x-1|表示数轴上实数x所对应的点到1和2所对应的点的距离之和,其最小值为1.
∴点M(2,3)到直线y=x+2的直角距离为1.
 (1)d(O,P)=|0-1|+|0-3|=4;
(1)d(O,P)=|0-1|+|0-3|=4;故答案为:4;
(2)∵O为坐标原点,动点P(x,y)满足d(O,P),
∴|0-x|+|0-y|=|x|+|y|=2,
所有符合条件的点P组成的图形如图所示;
(3)∵d=|x-2|+|y-3|=|x-2|+|x+2-3|
=|x-2|+|x-1|
∴x可取一切实数,|x-2|+|x-1|表示数轴上实数x所对应的点到1和2所对应的点的距离之和,其最小值为1.
∴点M(2,3)到直线y=x+2的直角距离为1.
看了 我们知道对于x轴上的任意两点...的网友还看了以下:
两个小球碰撞后的运动轨迹问题在平面内两个相同的小球AB发生碰撞,此时A坐标(X,Y),B坐标(x2 2020-04-27 …
两个小球碰撞后的运动轨迹问题在平面内两个相同的小球AB发生碰撞,此时A坐标(X,Y),B坐标(x2 2020-05-14 …
有关两向量相加后,得到向量的模与原来两向量的坐标的关系设向量a坐标为(x1,y1),向量b坐标为( 2020-05-14 …
一般情况下,如果一元二次方程ax^2+bx+c=0(a不等于0)的两个实数根分别为x1和x2,那么 2020-05-16 …
一直线与抛物线x2=y交与a、b两点,他们的横坐标分别为x1、x2,此直线在x轴上的截距为a,求证 2020-06-14 …
如图,二次函数y=-x2+nx+n2-9(n为常数)的图象经过坐标原点和x轴上另一点A,顶点在第一 2020-07-20 …
如图,在平面直角坐标系中,抛物线y=-x2+3x与x轴交于O、A两点,与直线y=x交于O、B两点, 2020-07-26 …
二次函数已知与X轴交于两点,怎么求函数解析式?请详细一点.忘了说,是只知道与X轴的交点两个坐标,( 2020-08-01 …
如图,在平面直角坐标系xOy中,点A坐标为(8,0),点B在y轴的正半轴上,且cot∠OAB=,抛 2020-08-02 …
想好久的数学题,大侠!若设关于X的一元二次方程ax²+bx+c=0(a≠00的两个根分别为X⒈,X2 2020-11-04 …