如图，在平面直角坐标系中，抛物线y=-x2+3x与x轴交于O、A两点，与直线y=x交于O、B两点，点A、B的坐标分别为（3，0）、（2，2）．点P在抛物线上，且不与点O、B重合，过点P作y轴的平行线交射

Question

如图，在平面直角坐标系中，抛物线y=-x²+3x与x轴交于O、A两点，与直线y=x交于O、B两点，点A、B的坐标分别为（3，0）、（2，2）．点P在抛物线上，且不与点O、B重合，过点P作y轴的平行线交射线OB于点Q，以PQ为边作矩形PQMN，MN与点B始终在PQ同侧，且PN=1．设点P的横坐标为m（m>0），矩形PQMN的周长为C．

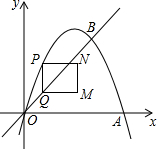
（1）用含m的代数式表示点P的坐标．
（2）求C与m之间的函数关系式．
（3）当矩形PQMN是正方形时，求m的值．
（4）直接写出矩形PQMN的边与抛物线有两个交点时m的取值范围．

Answer 1

（1）∵P在抛物线y=-x²+3x上，且点P的横坐标为m（m>0），
∴点P的坐标为：（m，-m²+3m）

（2）∵PQ∥y轴，
∴Q（m，m）．
①当0PQ=-m²+3m-m=-m²-2m，
C=2（-m²+2m）+2=-2m²+4m+2．
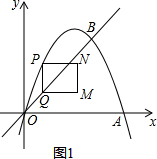
②当m>2时，如图2中，
PQ=m-（-m²+3m）=m²-2m，
C=2（m²-2m）+2=2m²-4m+2．

（3）∵矩形PQMN是正方形，
∴PQ=PN=1，
当0-m²+2m=1，解得m₁=m₂=1．
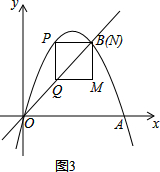
当m>2时，如图4中，
m²-2m=1，
解得m₁=1+√(2)，m₂=1-√(2)（不合题意舍弃）；

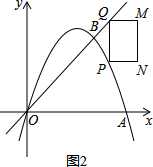
（4）由图3可知当m=1时矩形PQMN的边与抛物线有两个交点；
∵抛物线y=-x²+3x=-（x-(3)/(2)）²+(9)/(4)
∴顶点的坐标为（(3)/(2)，(9)/(4)），
当M点在抛物线上时，∵Q（m，m）．
∴M（m+1，m+1），
∴m+1=-（m+1）²+3（m+1），
解得m=2，
∴当(3)/(2)≤m<2时矩形PQMN的边与抛物线有两个交点；
当Q的纵坐标为(9)/(4)时，Q的横坐标为(9)/(4)，
∴此时P的横坐标为(9)/(4)，
∴当m≥(9)/(4)时矩形PQMN的边与抛物线有两个交点；
综上，当m=1或(3)/(2)≤m<2或m≥(9)/(4)时矩形PQMN的边与抛物线有两个交点．